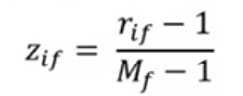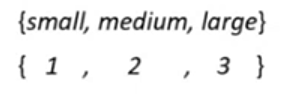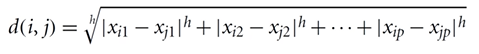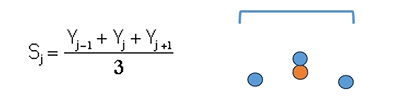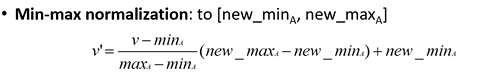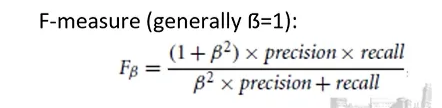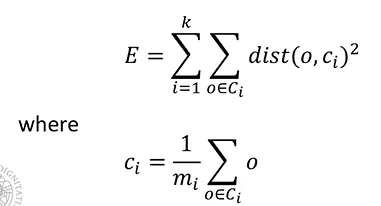Data Mining

Docente: Francesco Marcelloni [francesco.marcelloni@unipi.it] (Docente ML, Data Mining e Artificial Intelligence) Testo di riferimento: Data Mining: Concepts and Techniques. Morgan Kaufmann

Introduzione

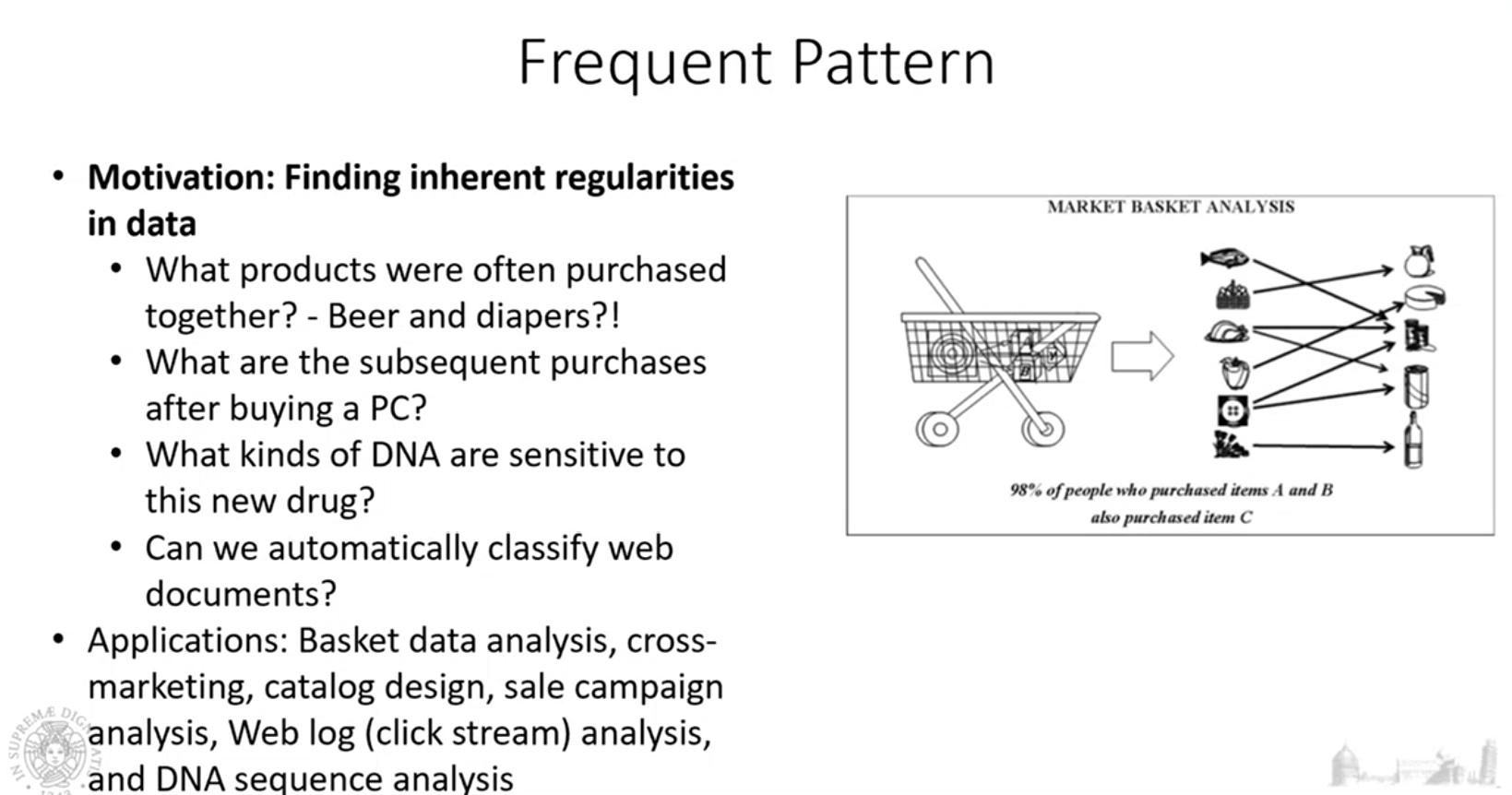
Data Mining: La pratica di andare a ricercare in grandi quantità di dati dei pattern, dei trend utili. (estrarre modelli)

Machine Learning

• Supervised Learning: Apprendimento attraverso l’etichettattura dei dati, definendone la supervisione nel processo di apprendimento, che creerà il modello utilizzato.
  • Modelli di Classificazione: modello che risolve problemi in cui l’output desiderato è poche possibilità (es. Email: Spam o non Spam, Capelli: Biondi o Mori o Rossi)
  • Modelli di Regressione: modello in cui l’output è un numero, quindi ci sono diversi possibili output.
• Unsupervised Learning: Apprendimento in cui i dati non vengono etichettati, lo scopo che si vuole raggiungere è quello di capire se possiamo raggruppare in qualche modo i dati a disposizione. Quindi individuarne dei pattern e dei modelli in questi dati.
  • Modelli di Clustering: Algoritmo che analizza l’insieme di dati non etichettati e ne individua i pattern a seconda delle caratteristiche del dato trattato (Es. Profilazione utenti)
• Reinforcement Learning: Apprendimento che inizialmente non ha bisogno di avere dati, l’apprendimento si basa sulla interazione di un agente (SW) e l’ambiente circostante (spesso utilizzato in robotica attraverso i sensori). Il modello apprendo effettuando delle azioni ed andando ad interpretare l’output/feedback ricevuto a seguito di quella determinata azione.

• Semi-supervised Learning: Utilizza l’Unsupervisioned Learning per clusterizzare i dati e poi utilizza il Supervised Learning per categorizzare i cluster individuati precedentemente.

  

Malware Detection

E’ possibile utilizzare il Data Mining per individuare malware all’interno di un sistema.

• Anomaly detection: tramite Data Mining si definisce un modello che riproduce il comportamento normale del sistema monitorato. Quando nel comparare il Modello “Virtuale” rispetto al sistema reale, il modella real differisce differisce molto, possiamo intuire possibili comportamenti anomali e quindi possibili malware.
• Misuse detection: identifica attacchi conosciuti creando un modello che si basa su esempi di attacchi precedentemente effettuati. Ciò avviene tramite Modelli di Classificazione (Supervised Learning).
• Hybrid approach: combina tecniche di Classificazione e di Anomaly detection per incrementare l’individuazione di possibili attacchi

Intrusion Detection

Agenti malevoli che cercano di eseguire attacchi informatici, possono essere individuati analizzando i log dei sistemi in modo da identificare possibili anomalie che corrispondono all’attacco.

Fraud Detection

Ad esempio analizzando come la carta di credito viene utilizzata solitamente, per individuare comportamenti anomali rispetto al normale utilizzo che viene fatta dalla carta di credito.

Ad oggi AI/ML trasformano il testo in vettori numerici:

• Ex. “Mouse”:
  • Significa sia topo che mouse del computer
  • Se analizzo solo la stringa il significato è bivalente
  • Cosa diversa è se riesco a rappresentare “mouse” nel contesto utilizzato, le tecniche attuali utilizzate da AI/ML consentono di trasformare “mouse” in un vettore numerico differente in base al contesto utilizzato.
  • Una volta che ho la descrizione numerica distinta in base al contesto posso applicare gli algoritmi di Data Mining.

Rappresentazione dei Dati

Viene definito data set un insieme di data object.

Object: una entità generica, come dati, utenti, oggetti venduti, pazienti etc.

• Ogni oggetto è descritto da un certo numero di attributi.
• Pensandolo in un DB, ogni oggetto corrisponde ad una riga della tabella, il singolo attributo alle colonne della tabella.

Attributo: è un campo che descrive una caratteristica dell’oggetto.

• Ex. Nome, indirizzo, Data di nascita, Matricola etc.

Principali tipi di attributi

Nominali:

• Attributo che definisce una categoria o uno stato o una “etichetta”
• questo tipo di attributi assume pochi valori (ex. colore dei capelli, zip code, occupazione)
• La distinzinone fra “etichetta” e valore numerico è che le etichette non sono ordinabili, mentre il valore numerico si.
• L’ordinamento non è un concetto banale, supponiamo di avere due oggetti “persona” descritte dagli attributi “colore occhi” e “colore capelli”. Vogliamo capire come misurare la distanza fra questi due oggetti, ovvero assumendo di avere molte persone, capire quali sono le persone più simili in base a questi due attributi. Per fare cià definisco come sege la distanza in base agli attributi nominali:
  • Avendo due oggetti $i$ e $j$, definiamo la distanza fra i due oggetti $d(i,j$) con la seguente formula $d(i,j) = (p-m)/p$
  • $p$: numero di attributi nominali presenti in ogni oggetto

  • $m$: numero di attributi nominali in cui i due oggetti hanno lo stesso valore

    Esemipio: p1 = (green, blond) p2 = (green, black)

    $d(p1,p2) = (2-1)/2 = 0.5$

Binari:

• Attributo in realtà nominale, poichè assume solamente valore $0$ o $1$
• Si distingue in attributo binario simmetrico e attributo binario asimmetrico:
  • Simmetrico: l’attributo 0 e 1 hanno la stessa probabilità di apparire
  • Asimmetrico: la probabilità di avere 0 è in generale molto più alta di avere 1, o viceveresa in alcuni casi.
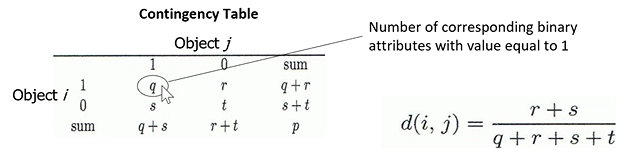
• La distanza fra due oggetti di tipo binario si calcola tramite formula di contingenza, costruendo la tabella di contigenza è possibile precedere come segue:

  $q$: definisce il numero di attributi nei due oggetti $i$ e $j$  che hanno valore $1$

$r$: definisce quanti attributi hanno valore $0$ nell’oggetto $j$ mentre nell’oggeto $i$ hanno valore $1$

$s$: definisce quanti attributi hanno valore $1$ nell’oggetto $j$ mentre nell’oggetto $i$ hanno valore $0$

$t$: definisce il numero di attributi nei due oggetti $i$ e $j$ che hanno valore $0$

$p$: definisce il numero totale degli attributi

Formala di contingenza:

$d(i,j) = (r+s)/(q+r+s+t)$

• Si noti che $(q+r+s+t) = p$
• La formula di contingenza si comporta uguale in caso di attributi simmetrici e asimmetrici, ma in casi pratici, quando abbiamo attributi asimmetrici:
  • $t$ assumerà valori molto alti
  • i due oggetti di conseguenza sembreranno molto vicini, ovvero molto vicini allo 0
  • Come ci comportiamo quindi in caso di attributi asimmetrici? non consideriamo $t$

  • la formula di continguenza diventa:

    $d(i,j) = (r+s)/(q+r+s)$

Ordinali:

• Attributo “etichetta”/nominale che ha possibilità di avere un ordinamento

• Ad esempio parlando di valori numerici, abbiamo la percezione della misura:

  $Size = {small, medium, large}$

• Vorremmo che questa percezione di ordinamento (small, medium, large) venga riportata nella distanza
  • Per farlo posso associare ad i valori possibili per l’attributo nominale, associamo numeri interi crescenti.
  • quindi in questo caso: 1 = small, 2 = medium, 3 = large
  • Successivamente mappiamo il range di ogni attributo nel range [0,1] ovvero normalizzaiomo il range. Quindi mappando i valori 1,2,3 in modo tale che il nostro attributo Ordinale abbia attributi tra 0 e 1.

  • Per fare ciò utilizzamo la formula:

    

    Dove:

    • $r_{if} \in {1, …, M_f}$ ovvero tutti i valori che l’attributo $r_{if}$ può assumere dopo l’associazione dei numeri interi crescenti alle “etichette”
    • $M_f$ = numero massimo di valori che $r_{if}$ può assumere, ovvero il numero totale di attributi dell’oggetto

  • In questo esempio:

    

    • $r_f$ = { 1 , 2, 3 } dove 1 = small , 2 = medium, 3 = large
    • $M_f$ = 3

    • ottenendo:

      

• Il vantaggio è che si passa da un attributo Nominale (small, medium, large) ad un attributo Numerico (0, 0.5 , 1).

Attributo numerico:

Quando parliamo di attributi numerici parliamo di:

• Valori Intervallari:
  • Misurati su scale “equal-sized units”
  • Non presentano il valore 0, non esiste il punto di 0 effettivo
  • Es. temperatura in gradi Celsius (C), lo 0 è uno 0 fittizzio, che non corrisponde allo 0 a livello di temperatura
  • Questo significa che in questo caso, possiamo applicare operazioni di sottrazione o di somma dato che hanno significato, ma non ha significato applicare operazioni di moltiplicazione o di divisione in quanto non esiste lo 0
• Valori razionali
  • Es. temperature in gradi Kelivn (K), lunghezze, quantità monetarie
  • Valori per cui esiste lo $0$ effettivo e di conseguenza è possibile effettuare operazioni di moltiplicazione o di divisione

Quando vogliamo calcolare la distanza tra oggetti descritti da valori numerici

• Possiamo applicare la distanza Minkopwski (simile a distanza euclidea se h = 2 o distanza di Manhattam se h = 1)

• dato che gli oggetti sono essenzialmente dei punti, descritti dagli $n$ attributi che rappresentano le $n$ dimensioni in cui tali punti possono essere rappresentati, utilizzando la distanza euclidea (h = 2) posso capire la distanza fra questi punti.

Quando un oggetto è descritto da diversi tipi di attributi, il calcolo della distanza diventa più complesso. In questo caso, si calcola la distanza per ciascun attributo e si effettua una media pesata, dove il peso è determinato dal numero di attributi di ogni tipo.

Misurare la dispersione dei dati

E’ in generale interessante capire la distribuzione dei valori degli attributi all’interno del dataset

Box Plot:

• Sfrutta il percentile, il K-esimo percentile di un set di dati numerici corrisponde al valore Xi in cui ho il K-percento dei restanti valori uguali o al di sotto Xi (es. la mediana corrisponde al 50-esimo percentile)
• il Box-Plot utilizza i Quartili, che esprime 25-percentili dove:
  • Q1 = 25-esimo percentile
  • Q2 = 50-esimo percentile
  • Q3 = 75-esimo percentile
  • Q4 = 100-esimo percentile

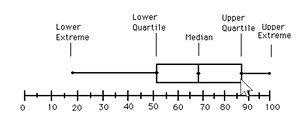
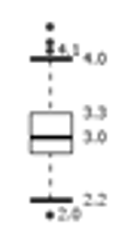
• il Box-Plot viene utilizzato per rappresentare la distribuzione dei valori numerici all’interno di un attributo numerico.

  

  • Lower extreme = minimo;
  • Lower quartile = Q1;
  • Median = Median;
  • Upper quartile = Q3;
  • Upper extreme = massimo;
  • Whiskers: le due linee fuori dalla box;

  

  Outlier: astersichi nel grafico, sono punti considerati molto differenti dagli altri punti presenti nel dataset

Analizzando un Box-Plot posso capire dove sono concentrati i punti, e soprattuto come è la dispersione dei punti all’interno dell’attributo stesso

Istogramma:

Altra possibilità è quella di utilizzare l’istogramma, in quanto analizza la frequenza di quei range di valori nel mio insieme di dati.

• Differenza tra Istogramma e Barchart è che nell’istogramma non ci interessa l’ampiezza, ma l’area della barra che sta ad indicare la frequenza del valore numerico. Nel barchart invece è l’ampiezza il valore interessante. Normalmente non si distingue barchart da istogramma, perché tendenzialmente area ed ampiezza mi danno la stessa informazione, ovvero osservo l’istogramma come se fosse un barchart ribaltato.
• L’istogramma consente di avere un dettaglio molto più preciso, in quanto il box-plot si esprime in quartili.
• Box-Plot e Istogramma ci danno una idea di come i valori degli attributi son distribuiti
• Come possiamo capire se avendo due attributi, se in un attributo aumenta il valore aumenta anche nell’altro attributo? oppure se uno cresce e l’altro decresce? si attraverso lo Scatter Plot

Scatter Plot:

• Prendo gli oggetti e vado a disegnare in un piano cartesiano con i valori degli attributi degli oggetti che sto considerando
• Possiamo costruire uno Scatter Plot usando un attributo sulle ascisse e uno sulle ordinate e rappresentando i punti nel piano che si forma.

• gli Scatterplot sono molto interessanti, perché consentono di capire in modo semplice se esiste una relazione tra i 2 attributi. Infatti se ho due attributi che descrivono il mio oggetto, che sono fortemente correlati, posso concludere che i due attributi hanno un uguale contenuto informativo, ovvero potrebbero essere ridondanti per il problema che voglio risolvere. Quindi se faccio un’analisi di correlazione e noto che due attributi risultano fortemente correlati posso decidere di non considerare uno dei due attributi.

  

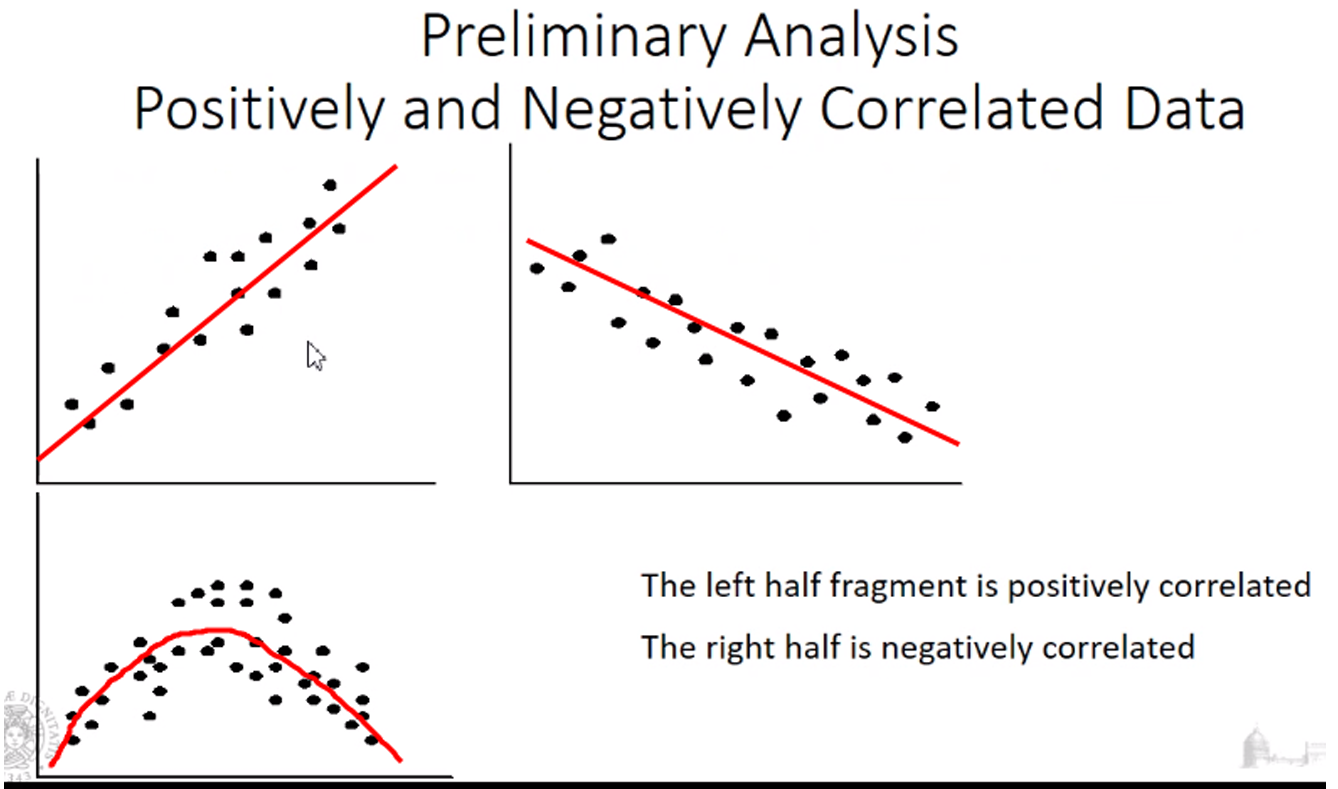
  • Nel primo scatter plot all’aumentare del valore della x aumenta anche la y, lo scatter plot è molto concentrato all’interno di una linea.
  • Nel secondo otteniamo invece un fenomeno inverso.
  • Questi 2 scatter plot ci fanno capire che esiste una correlazione tra i 2 attributi, all’aumentare del valore di un attributo aumenta anche l’altro o vicersa, quindi i 2 attributi hanno una quantità informativa simile, ovvero il trend è lo stesso.
  • Se hanno uno stesso trend, due attributi probabilmente hanno lo stesso valore informativo. Potremmo pensare quindi di non usarli entrambi dal punto di vista di tecniche di data mining, decidendo di usarne uno solo.
  • Nel caso dello scatter plot in basso invece è ovviamente differente in quanto la distribuzione dei punti non si muove lunga una linea, ma vi è una correlazione positiva fino a un certo valore della x e poi da quel valore in poi la correlazione diventa negativa.

Questa analisi di correlazione attraverso scatter plot può essere utile per farci capire che ci sono coppie di attributi ridondanti. La produzione di scatter plot può avvenire solo per attributi di tipo numerico.

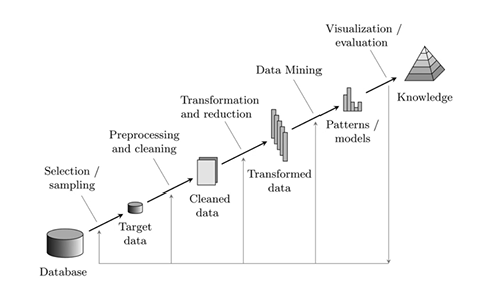
Processo di Datamining

Qualsiasi sia il problema che vogliamo risolvere si segue il processo mostrato sopra:

• Partiamo da un insieme di dati da cui vogliamo estrarre una nuova conoscenza, come pattern o modelli.
• Selection/sampling e Preprocessing and cleaning: Individuati i target data e raccolti i dati, tali dati possono essere inconsistenti, ridondanti, non puliti. dunque è necessario ripulirli in modo da essere “omogenei”
• Transformation and reduction: trasformare i dati normalizzando gli attributi e eliminando gli attributi ritenuti ridondanti o non necessari. Trasformaimo gli attributi anche normalizzandoli i range dei valori degli attributi rendendoli più comodi per l’analisi, ad esempio normalizzandoli a 0 e 1

Data Cleaning

Pulizia del rumore all’interno dei nostri dati

Casi ricorrenti

• dati incompleti: caso in cui alcuni degli attributi che definiscono il data object è mancante. Ciò può rappresentare un grande problema poiche inquina il nostro algoritmo che calcola la distanza tra i nostri data object
• dati “rumorosi”: caso in cui alcuni dei nostri valori presentano errori, valori non aspettati, outliers all’interno dell’attributo.
• dati inconsistenti: caso in cui gli attributi degli oggetti vanno in conflitto fra di essi, fra attributi che esprimono la stessa informazione ma con valori differenti. Inconsistenze possono capitare anche quando si uniscono due database/dataset in cui non vegnono mantenute delle convenzioni, ad esempio quando si uniscono database generati in italia rispetto a quelli inglesi, in italia usiamo i metri in inghilterra i pollici e magari nell’attributo non viene specificata l’unità di misura, rendendo i dati inconsistenti.
• dati intenzionalmente rumorosi: caso in cui il dataset decide di fare alcune forzature sugli attributi, ad esempio associando un valore di default che però non corrisponde al valore corretto.

Dati incompleti, come risolvere il problema?

Tre approcci principali:

• ignorare l’oggetto avente attributo mancante: Approccio che va bene se la percentuale di oggetti con valori mancanti è irrisorio rispetto al dataset totale. Se invece la percentuale è alta ciò mi cambia la distribuzione dei dati, rendendo il modello/ il dataset non affidabile.
• Riempire il valore dell’attributo mancante a mano: Approccio poco attuabile, poiché ad oggi i dataset contengono moltissimi dati, quindi impossibile riempire manualmente i valori mancanti
• Rimpeire i valori dell’attributo in maniera automatica, con diversi approcci in base al caso:
  1. Approccio che va ad inserire il valore “unkonwn” o una costante all’attributo con il valore mancante. Ciò è per segnalare esplicitamente che lì c’è un valore mencante.
  2. Nel caso di attributi numerici solitamente si inserisce la media dei valori di quell’attributo.
  3. in caso di classificazione ogni oggetto avrebbe una classe associata, invece della media dell’attributo in maniera generale, potrei considerare la media dell’attributo solamente della classe interessata, in questo modo affino la media rendendo il valore meno dispersivo.
  4. Provare ad inferire quel valore rispetto ai valori adiacenti o vicini al dato, ciò può essere fatto attraverso (nuovamente) un processo di datamining

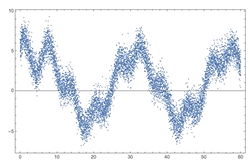
Dato rumoroso, come risolvere il problema?

Quando applichiamo dei filtri per ridurre il rumore, è bene stare attaenti ad individuare il nostro obiettivo. Se dobbiamo pulire il dato va bene applicare il filtro, ma dobbiamo stare attenti ad applicare il filtro se vogliamo individuare gli outlier, il filtro li farebbe perdere.

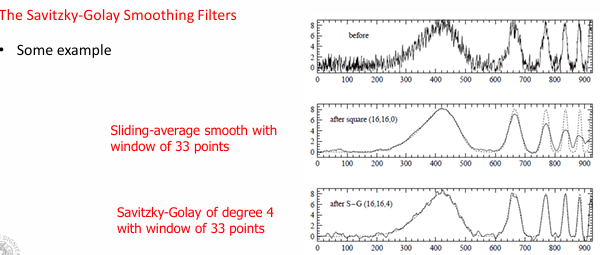
Filtro di smoothing rettangolare: “arrotondano il segnale” si stabilisce una finsetra, ovvero un numero di campione, in cui si vuole applicare il filtro. Il filtro sostituisce il campione centrale, con la media dei tre campioni.

Filtro di smoothing su finestra di 3 campioni

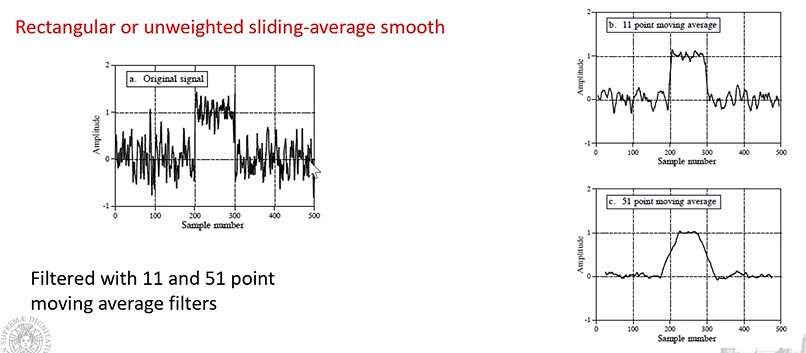
L’effetto che si ottiene:

Dalla immagine sopra, si può osservare quanto la finestra selezionata incida, nel caso del filtro a 51 campioni notiamo come il nostro segnale cambi significativamente rispetto a quello di partenza, a differenza del filtro con ampiezza di 11 campioni.

Quindi più è ampia la finestra più abbiamo un effetto di “smoothing” ma allo stesso tempo più è grande più rischiamo di alterare il segnale stesso, o il nostro dataset.

Anche qui ovviamente l’efficacia dell’applicazione del filtro con una determinata ampiezza dipende dal nostro obiettivo.

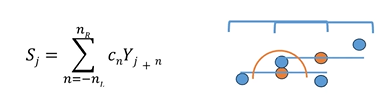
Filtro di Svitzky-Golay (generalizzazione del filtro rettangolare)

calcolo di una media pesata dei campioni che si trovano all’interno della finestra.

Nl = numero dei campioni a sinistra del nostro data point

Nr = numero di campioni a destra rispetto al nostro data point

Cn:

• se considero Cn un valore costante, ottengo il solito filtro rettangolare, traducendosi nell’approssimazione del campione con una “linea”(nel caso del segnale) parallela rispetto all’asse X.
• posso utilizzare dei polinomi di diversi ordini, ciò consente di modellare in maniera più ampia come si muovono i campioni all’interno della nostra finestra

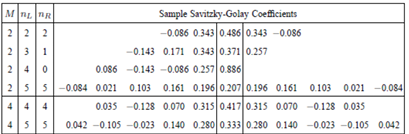
Per far ciò Savitzky-Goley hanno definito dei cofficenti ottimali che possono essere utilizzati all’interno del nostro modello a seconda del polinomio scelto

La cosa interesante è che questi coefficenti una volta calcolati “offline” i polinomi desiderati posso calcolarmi questi polinomi ed utilizzarli direttamente durante l’applicazione del filtro.

Con l’applicazione del Savitzky-Goley non ho una riduzione dell’ampiezza del segnale a seconda dell’ampiezza della finestra scelta. ciò avviene grazie alla descizione del polinomio.

Qual è la seclta ottimale?

si applica un rapporto, fra l’ampiezza del picco e l’ampiezza della finestra denominato smoothing ratio

• se obiettivo della misura, è di misurare altezza e larghezza del picco, allora dovremmo adottare degli smoothing ratio inferiori a 0.2
• se obiettivo è misurare la posizione del picco possiamo utilizzare smoothing ratio più alti di 0.2

Quando non dovrei utilizzare il filtro di smoothing?

• se voglio individuare degli outlier, è bene non applicare dei smoothing filter

Data discrepancy detection:

Come posso comprendere se il valore di un attributo è un valore possibile e quindi non sporco?

• tramite l’uso dei metadati:
• posso fare alcuni check:
  • uniqueness rule: il valore attrobuti all’attributo per ogni dataset deve essere univoco e divverente.
  • consecutive rule:
  • null rule:
• Posso utilizzare dei tool:
  • Data scrubbing:
  • Data auditing: strumenti che riescono a scoprire delle possibili inconsistenze basandosi su alcune regole e relazioni, ad esempio posso scoprire se due oggetti o attributi sono ridondanti

Ridondanza:

• Replicazione degli attributi: lo stesso attributo o oggetto ridondante
• Attributi derivati: un attributo che si può derivare da un’altro attributo, questo indica che probabilmente che uno dei due è eliminabile

Analisi di correlazione

Obiettivo di individuare attributi ridondanti, in modo da eliminare attributi ed oggetti ridondanti non modificando l’output del nostro modello.

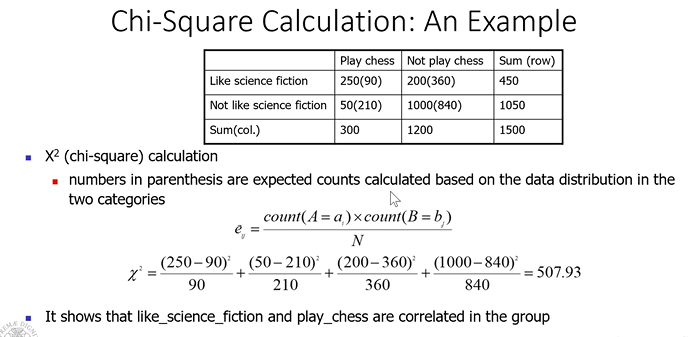
Chi-square: strumento statistico che consente di analizzare la possibile correlazione fra due attributi nominali.

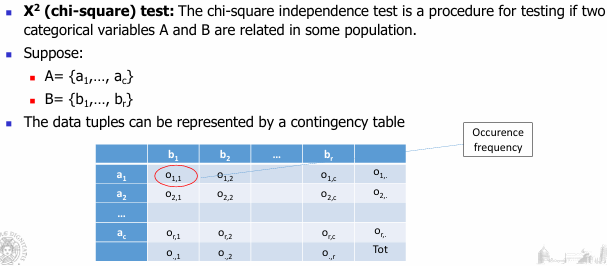
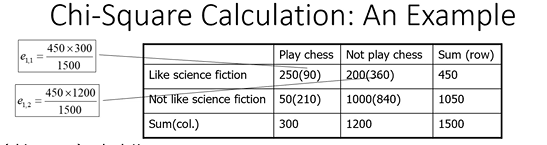
Si basa sulla tabella di contingenza:

• righe: possibile valori di attrobuta A
• colonne possibile valori degli attributi B
• nella cella troviamo il numero di istanze in cui i due attributi A e B hanno il valore specificato nella righa e colonna

Chi-square viene calcolato tenendo in considerazione il i valori osservati e valori expected, mantenendo l’ipotesi che i due attributi siano correlati. Infatti Expected viene calcolato presupponendo che i due attributi siano correlati:

• Se X^2 (chi-square) è molto piccolo, vicino a 0, i due attributi sono indipendenti, quindi devo lasciarli entrambi.
• Se X^2 (chi-square) è molto grande, posso dedurre che i due attributi sono correlati e quindi molto probabilmente uno dei due è ridondante e quindi eliminabile

Esempio:

Ma come decido se il valore di chi-squared rappresenta due attributi effettivamente correlati?

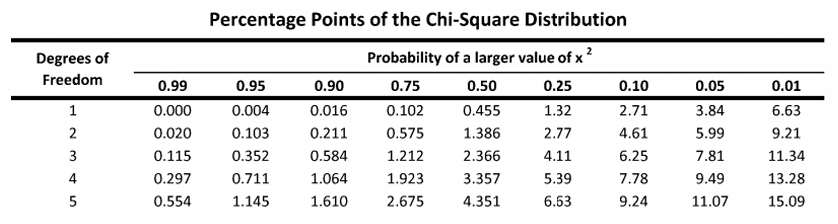
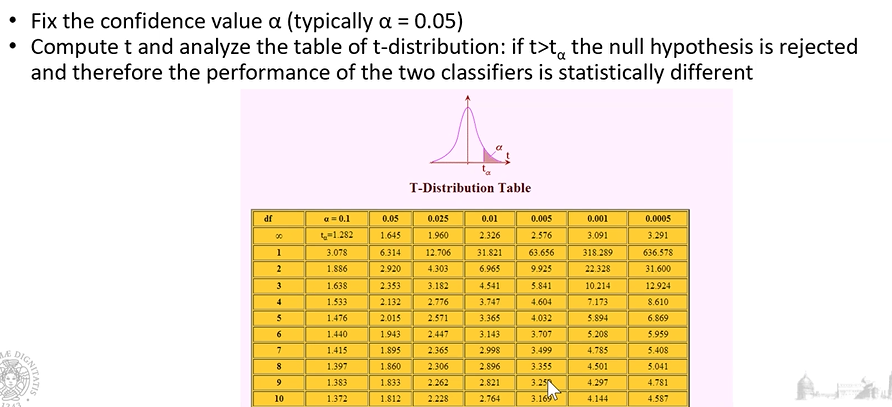
Da un punto di vista statistico, identifico il livello di confidenza e definisco i gradi di libertà, che i ottengono moltiplicando il numero di valori - 1 x il numero dei valor del secondo attributo - 1:

nel caso specifico il grado di libertà è 1, identifico il grado di confidenza e leggo il numero

se il valore che calcolo è maggiore del valore nella tabella posso affermare che i due attributi sono correlati con una confidenza statistica che ho fissato quando identificato il livello di confidenza.

Coefficente di Pearson (caso Attributi numerici)

divido per Numero di Oggetti deviazione standard A deviazione standard B

• Se coeff è maggiore di 0, gli attributi sono correlati positivamente
• se coeff = 0, gli attributi sono indipendenti
• se coeff minore di 0, gli attributi sono correlati negativamente

l’analisi che possiamo fare con questo cefficiente, possiamo evincere se questi attributi hanno in qualche modo una informazioni simile, quindi alta correlazione, e quindi decidere ti eliminare uno dei due attributi.

Data Reduction

• Riduzione della dimensionalità: impatta sia l’efficienza e ma soprattutto sui risultati che posso ottenere, infatti quando ho molte dimensioni tutti i punti appaiono lontani fra di loro, quindi non clusterizzabili. ridurre il numero di dimensioni ci aiuta su questo problema.
• Riduzione della numerosità: impatta solamente sull’efficienza e dunque ridurre i tempi computazionali
• Data compression:

come posso ridurre la dimensionalità?

Principal Component Analysis (PCA)

Trasformazione per cui si parte dallo spazio iniziale e si cerca una trasformazione, in modo da avere un nuovo spazio (nuovi assi) lungo i quali i dati che ho, se li proietto sul nuovo asse hanno valori separati (se si sovrappongono vuol dire che l’asse non rappresenta una dimensione rilevante).

Dal punto di vista matematico la PCA definisce una matrice con autovettori che rappresentano le dimensioni analizzati e autovettori che rappresentano la variabilità degli oggetti all’interno dello spaziio. Applicando la PCA elimino gli autovettori che hanno una bassa variabilità, lasciando quindi solo gli autovettori rilevanti aka le dimensioni utili ad analizzare il mio dataset.

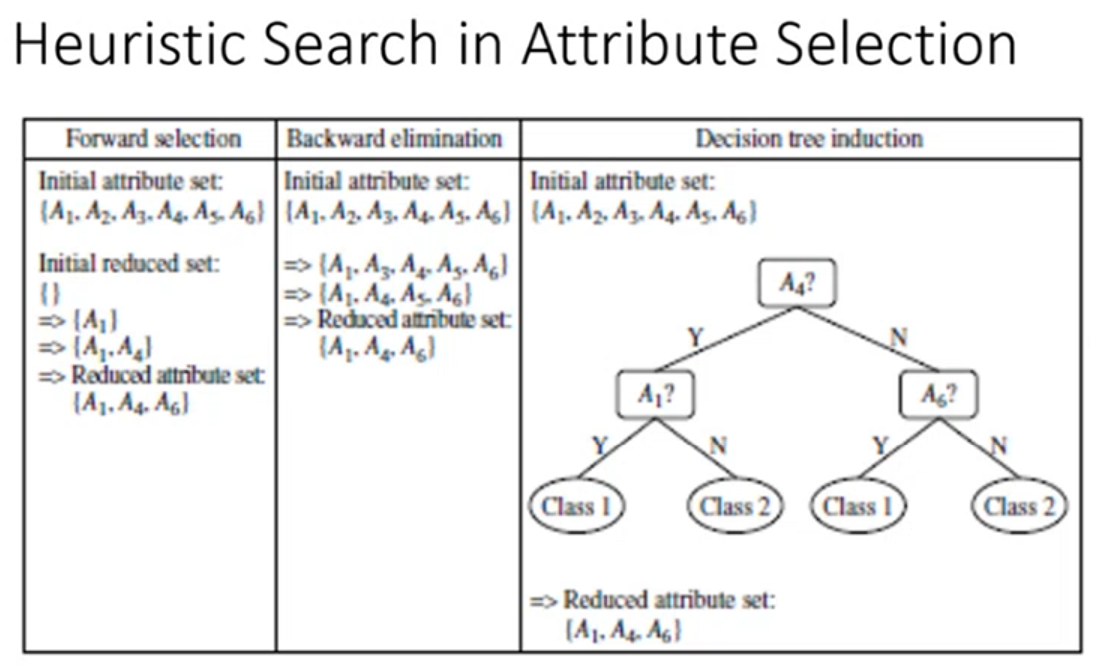
Heuristic Search in Attribute Selection

un’altra tecnica per ridurre il numero di caratteristiche agisce direttamente nello spazio originale

• Forward selecetion: parto da un insieme iniziale di caratteristiche selezionate vuoto, e ad ogni iterazione vado a selezionare l’attributo che ritengo migliore per quella iterazione. Per capire qual è l’attributo migliore da selezionare devo introdurre una metrica, una misura per comparare gli attributi.
• Backward elimination: parto avendo tutti gli attributi in un insieme, e ad ogni iterazione elimino l’attributo che ritengo peggiore. Anche qui per capire qual è l’attributo peggiore è necessario introdurre una metrica.
• Decision tree: non è un selettore di caratteristiche ma è a tutti gli effetti un classificatore, che implicitamente fa selezione delle caratteristiche.

Esempio Forward Selection [video seconda lezione]

Riduzione della Numersità: SAMPLING

Prendo i miei oggetti a campione, gli oggetti devono essere una rappresentazione abbastanza stabile del nostro dataset originale.

• simple random sampling
• campionamento senza rimpiazzamento: una volta che l’oggetto è selezionato, viene rimosso dal dataset. All’estrazione successiva l’oggetto non è più presente.
• campionamento con rimpiazzamente: l’oggetto selezionato non viene rimosso dal dataset, quindi all’estrazione successiva potrebbe uscire nuovamente lo stesso elemento.
• campionamento stratificato: riportare nella popolazione ridotta esattamente le stesse proporzioni delle classi di quelle che avevo nella popolazione iniziale.

Data Transformation

normalizzazione:

min-max normalization: fisso un range di variazione a cui voglio portare il mio attributo, es voglio far variare quell’attributo tra 0 e 1

Questa normalizzazione può generae un problema, in caso di un outlier (quindi o val min o val max) quando applico la formula, i valori vengono schiacciati in piccoli range, aka non ho una scala veritiera.

Z-score normalization (risolve problema dell’outlier):

Quando applico z-score normalization gli attributi non variano nello stesso range a differenza della normalizzazione min-max che definisce i valori di normalizzazione.

Classificazione

Obiettivo: ad ogni oggetto vogliamo associare una classe

Partiamo da un set di dati classificati, arriva un nuovo oggetto e devo riuscire a classificare l’oggetto.

Classificatore base: se il nuovo oggetto coincide perfettamente con un oggetto presente nel set di addestramento, associo l’oggetto alla classe dell’oggetto presente nel set. Se non coincide a nessun oggetto dico che non sono in grado di classificarlo.

Lazy Learners

1-nearest neighbours: classificazione in base all’oggetto più simile vicino all’oggetto introdotto

k-nearest neighbours: classificazione in base ad un insieme di k oggetti vicini all’oggetto introdotto, k si definisce essenzialmente facendo delle prove. E’ una tecnica complessa da un punto di vista computazionale perché bisogna calcolare la distanza dell’oggetto introdotto rispetto a tutti i punti del dataset

• Per risolvere il problema della complessità computazionale possiamo pensare di ridurre il nomero di oggetti del nostro training set:
  • Sampling: creazione del training set tramite campionamento del training set iniziale
  • Replace: rimpiazzare un numero n di oggetti con un singolo oggetto rappresentativo di quell’insieme di oggetti

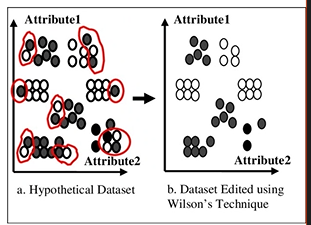
  • Editing: cerchiamo di ridurre il numero di oggetti ma pensando anche ad un possibile miglioramento del nostro training set, ovvero togliengo gli oggetti considerati inutili:

    

    • la tecnica di Wilson utilizza il classificatore stesso:

    

    • applichiamo all’oggetto analizzato il K-nearest neighbor, se la classe identificata coincide con la classe precedentemente assegnata all’oggetto analizzato, allora manteniamo l’oggetto
    • Se invece il K-nearest neighbor ci restituisce una classe differente dalla classe già assegnata all’oggetto analizzato, andiamo ad eliminare l’oggetto analizzato, in quanto probabilmente è un oggetto che crea rumore nel nostro training set

Grandi problemi di memoria dato che questi approcci devono analizzare tutto il training set

Eager Learners

Creo un modello Classificatore ed utilizzo direttamente il Classificatore senza necessità di basarmi nuovamente sul training-set come nel caso dei Lazy Learners.

• Il modello tipicamente è piuttosto semplice a livello computazionale, quindi tali modelli possono essere eseguiti in maniera molto rapida
• Dobbiamo però stimare l’accuratezza del modello nel classificare i nostri oggetti, par fare ciò:
  • Mi creo un insieme di test (test-set), diverso dal mio training-set, in cui conosco già la classe corretta dell’oggetto e che utilizzo per valutare il classificatore, ed esprimere la sua accuratezza
  • L’accuratezza è la percentuale di campioni nell’insieme di test che sono stati classificati correttamente nell’insieme di test
  • Classificatore in over-training: Quando l’accuratezza del classificatore sul training-set è molto più grande dell’accuratezza del classificatore sul test-set, questo significa che il classificatore è in over-training, ovvero il nostro classificatore non lavorerà bene su nuovi oggetti

Metodologie di costruzione del Modello di Classificazione:

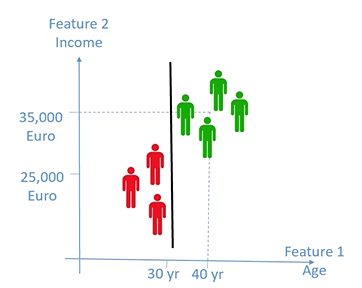
• Support Vector Machine/separation line:

  

  • Fondamentalmente vado ad utilizzare come modello l’equazione di una linea, in cui gli oggetti che ricadono da un lato o dall’altro lato del piano per classificare l’oggetto

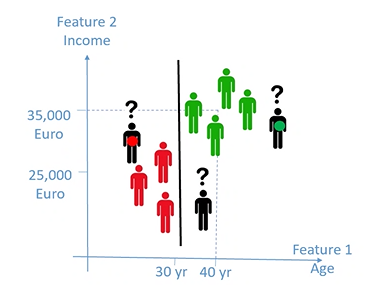
  • Si crea un problema però:

    

    utilizzando la linea classifico erronamente il nuovo oggetto

  • Il piano/linea che separa le mie classi deve essere infatti costruito in modo tale da trovare la linea ottimale che divide in maniera equidistante le classi

    

  • Questo classificatore funziona solamente se le mie classi sono linearmente separabili, questo difficilmente accade nella realtà
  • Le Support Vector Machine, sono applicabili solo a problemi con due classi, per ovviare ciò posso però applicare il piano individuato sulle n dimensione in base alle n classi dell’oggetto in fase di classificazione

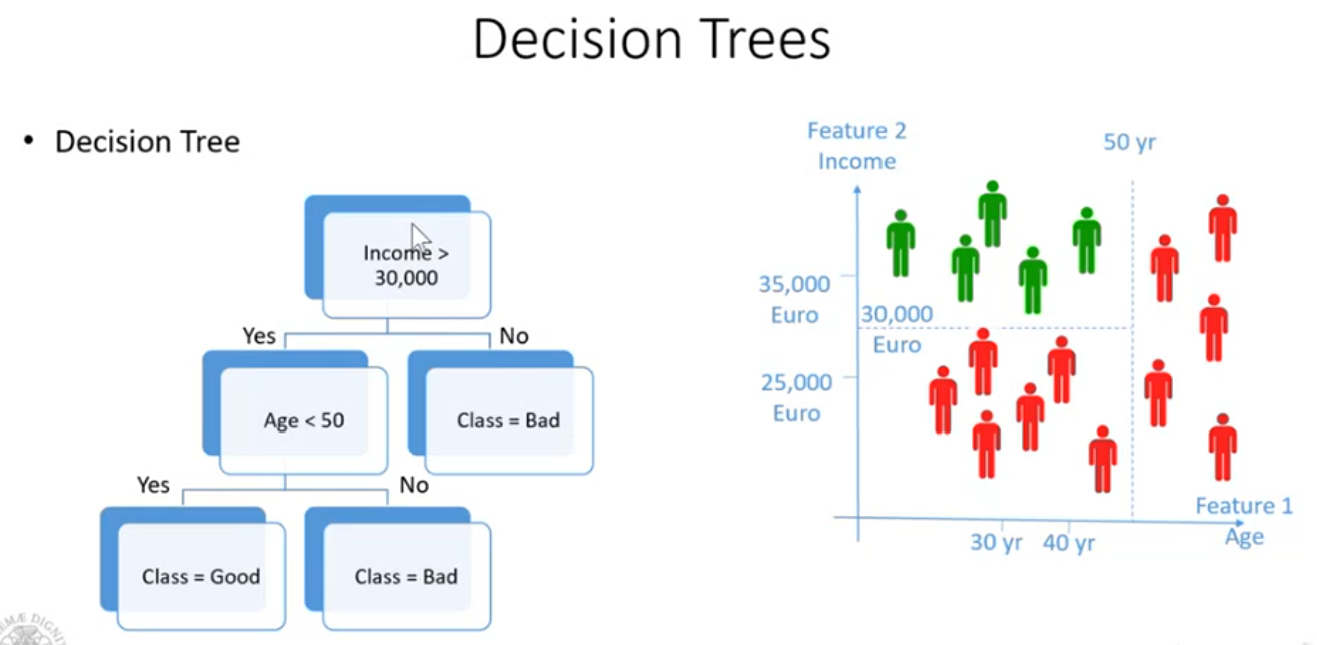
• Decision Tree:

  

  • classificatore explainable, consente di capire come prende la decisione finale sulla classe
  • abbiamo un nodo, chiamato nodo radice, ogni nodo rappresenta una decisione che viene presa sul valore di un attributo.
  • Le foglie rappresentano le classi.
  • Quando viene ricevuto un oggetto da classificare, si considera di navigare l’albero partendo dalla radice.
  • La cosa interessante è che quando vado a classificare un oggetto, è come se stessi spiegando come il classificatore sta prendendo la sua decisione.
  • Ma come estraggo il modello?

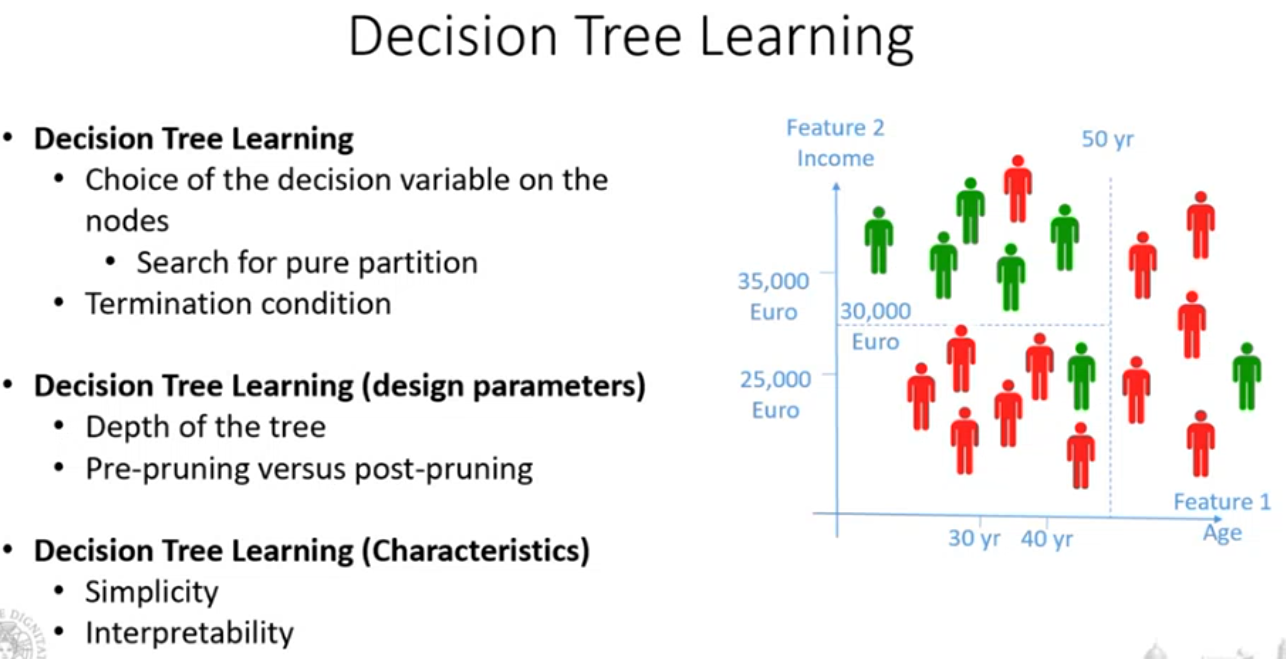
Decision Tree Learining

Algoritmo che mi deve consentire di capire quali sono gli attributi che devo utilizzare nei nodi di decisione, e qual è l’ordine di questi attributi da considerare, ovvero quale attributo devo mettere nel nodo radice e quali nelle sue successive ramificazioni.

L’idea è quella di cercare di selezionare gli attributi in modo ad arrivare ad ottenere dei sottospazi in cui ho un’unica classe.

Nel mondo reale non sempre riuscirò a trovare un sotto-spazio in cui ho un’unica classe, quello che succede però è che finendo gli attributi, inserirò una foglia, quindi classificando l’oggetto, che ha una classe maggoritaria dei punti che cadono nel sotto-spazio.

Vediamo che l’algoritmo costruisce l’albero in maniera ricorsiva, ad ogni livello cerca di prendere la decisione ottimale per quel livello.

1. parto con nodo radice con tutti gli attributi dell’oggetto
2. inizio cercando di individuare un attributo fra quelli presenti che mi consende di dividere il nodo radice in più nodi.
3. L’attributo viene scelto in modo che tale attributo riesca a dividere il nostro insieme in sotto-insiemi più “puri” possibili, ovvero aventi istanze appartenenti alla stessa classe.

L’algoritmo termina quando:

1. Tutte le istanze appartenenti ad un nodo appartengono ad una stessa classe. Qui sarebbe inutile continuare a dividere il nodo.
2. Ho terminato gli attributo e non ho possibilità di dividere ulteriormente il sotto-spazio, seleziono quindi la classe maggioritaria fra le classi appartenenti a quell’insieme
3. Ho terminato le istanze da suddividere

Come scelgo l’attributo?

• Entropia dell’informazione:
  • Supponiamo di avere n classi
  • Supponiamo di poter stimare la probabilità di ogni classe, contando il numero di istanze della classe analizzata, diviso il numero totale degli oggetti nell’insieme di addestramento

  • l’Entropia si calcola come segue:

    

    Asse Y: valore dell’entropia

    Asse X: valore della probabilità della classe rappresentata

  • Entropia = 0, significa che ho un insieme o sottinsieme di addestramente con un’unica classe
  • Entropia = 1, si ottiene quando ho uguale probabilità per le due classi che sto considerando, non ho una prevalenza di una classe su un’altra

L’idea è quindi quella di andare a selezionare, nella costruzione del nostro Decision Tree, gli attributi che mi generano l’entropia minore.

Cerco quindi l’attributo che mi dia il guadagno maggiore (Gain()), calcolo l’entropia nel mio dataset iniziale, decido un attributo, vedo l’attributo come divide in sottoinsiemi il mio insieme di dati e vado a vedere in ogni sottoinsieme qual è l’entropia che ottengo.

Andrò a selezionarà l’attributo che mi consente di ottenere il guadagno più alto.

Ad esempio:

Performance Evaluation

Per effettuare una valutazione di performance abbiamo bisogno di un insieme di test con le etichette/le classi per ogni istanza.

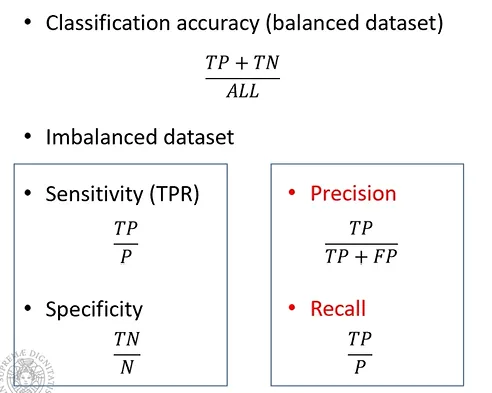
La metrica più intuitiva che ci viene in mente è l’accuratezza della classificazione:

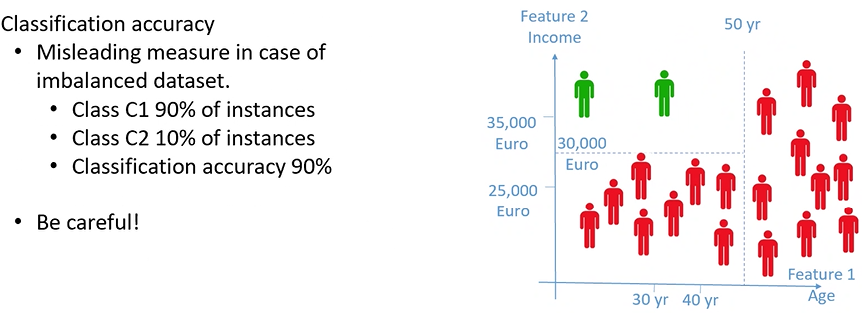
Sembra possa essere adatta, vediamo però un esempio:

Notiamo che il dataset è sbilanciato, ovvero c’è una classe a cui appartengono la maggior parte delle istanze, e una seconda classe in cui appartengono il minor numero di istanze.

In questo caso, seguendo i calcoli troveremmo che l’accuratezza è al 90%, nel caso che stiamo considerando però, dato lo sbilanciamento del dataset, anche un classificatore in cui qualunque istanza presentata venga classificata a C1 sarebbe comunque un classificatore con accuratezza al 90%. Ciò ci fa intuire come l’accuratezza non ci faccia capire realmente cosa accade nel classificare in quanto è fortemente orientata alla classe maggioritaria.

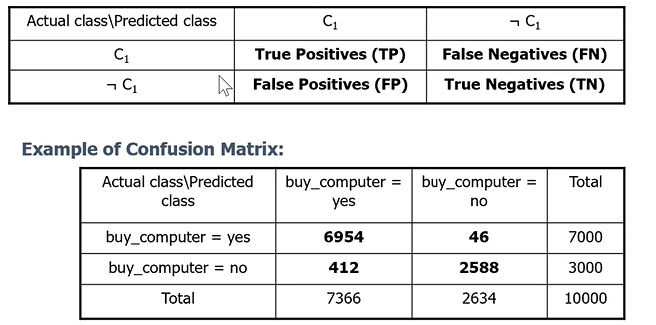
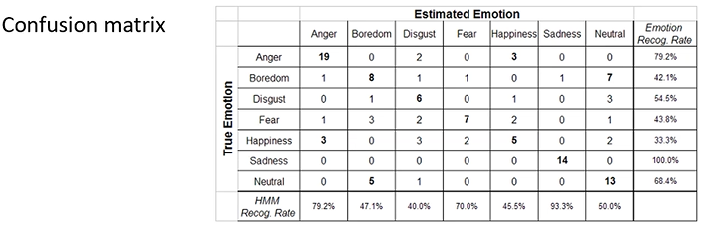
Matrice di confusione

Costruiamo una matrice di confusione definita nella immagine sopra:

• TP: Istanze Classificate come C1 e che sono appartenenti a C1
• FP: Istanze Classificate come C1 e che non sono appartenenti a C1
• FN: Istanze Classificate non come C1 che invece sono appartenenti a C1
• TN: Istanze Classificate come non C1 che non sono appartementi a C1

Notiamo quindi che una matrice ottimale, in cui un classificatore lavora in maniera ottimale, sarà una matrice diagonale in cui FN e FP sono a 0.

Confronto tra Matrici di confusione

Confrontare Matrici di confusione non è banale, per fare ciò quindi viene fatto come segue a seconda se il dataset è o meno bilanciato:

i range di questi parametri oscillerà tra 0 e 1.

• Sensitivity: 1 se la classificazione è ottimale nella classificazione delle classi “in positivo”; 0 se nessuna istanza è stata classificata “positivamente” correttamente
• Specificity: 1 se la classificazione è ottimale nella classificazione delle classi “in negativo”; 0 se nessuna istanza è stata classificata “negativamente” correttamente

Notiamo quindi come sia Sensitivity e Specificity siano necessarie per capire la qualità del nostro classificatore.

Stesso discorso vale per Precision e Recall

F-measure

Per confrontare due classificatori possiamo quindi calcolare crearci la nostra matrice di confusione per poi clacolare Precision e Recall poi misurare la F-measure

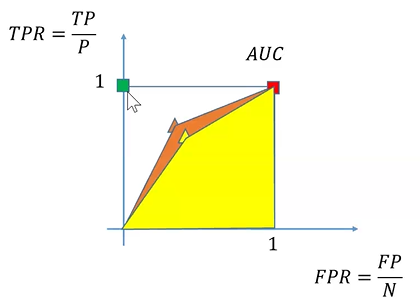
Ogni classificatore, può essere rappresentato in un piano denominato ROC:

Due classificatori rappresentati nel grafico dal punto/triangolino arancione e giallo, una volta testati con nostro insieme di test e generata la matrice di confusione, possiamo rappresentare i nostri classificatore in un piano ROC, in cui:

• Asse X : FPR , ovvero il rapporto fra FP e N
• Asse Y : TPR, ovvero il rapporto fra TP e P

Notiamo che il classificatore ideale avrebbe:

• FPR = 0
• TPR = 1

Quindi sul piano ROC il classificatore ideale corrisponderebbe al punto verde che vediamo nel grafico sull’asse Y.

I nostri classificatori invece sono due punti distinti rappresentati dai triangolini, per rappresentarli creiamo un poligono unendo il punto del classificatore a (0,0) e (1,1). Il classificatore che con l’area più grande (AUC) sarà quello maggiormente tendente al classificatore ottimale

Performance Evaluation on Multi-class problems

Per andare a calcolare TP TN TP e FN rispetto ad una singola classe C_i, consideriamo la classe C_i come la classe “positiva” mentre le restanti classi come classi “negative”, riportando il problema ad un problema a due variabili come visto prima.

K-Fold

avere una singola prova di performance evaluation su un singolo data-set per il nostro classificatore, potrebbe non essere sufficiente a valutare la qualità del nostro classificatore.

Per ovviare ciò dovremmo avere più data-set, e utillizzarli parte per training-set altri per effettuare i nostri test.

Per fare cià utilizzamo quello che viene chiamato k-fold:

T-Test

Supponiamo che le varianze di questi valori non siano molto differenti fra i vari folds, in questo caso possiamo utilizzare il t-test:

Wilcoxon test

Nel caso in cui non abbiamo nessuna assumption, possiamo utilizzare il wilcoxon test

Classificazione nel mondo reale

Oggi si tende ad utilizzare il Deep Learning, ovvero con approccio a molteplici layer, in cui tanti livelli di neuroni connessi fra di loro fa un’azione in particolare. Questi modelli sono potenti perché aumentando i parametri dati dalla molteplicità dei layer, essi si possono tarare per risolvere i problemi in considerazione. Tali modelli necessitano però di moltissimi dati.

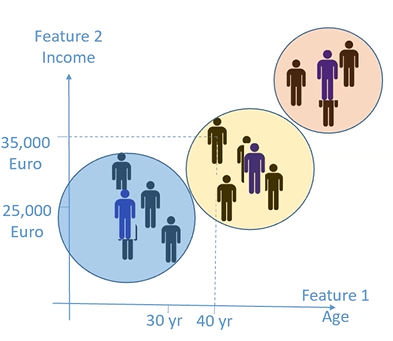
Clustering

Prendendo un insieme di oggetti, ognuno descritto da attributi e features ma non posseggono alcuna etichetta.

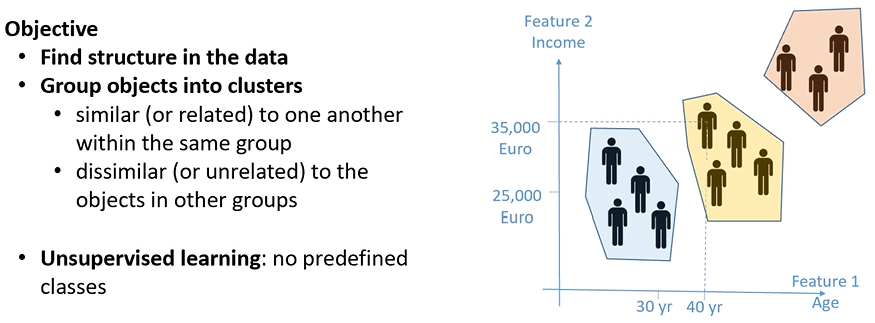
Lo scopo del clustering è quello di capire se riusciamo a trovare una qualche struttura nei dati e quindi riuscire a raggrupparli secondo un qualche criterio.

Generalmente, oggetti che sono simili tra di loro dovrebbero trovarsi nello stesso gruppo:

• Quando è che due oggetti si possono considerare simili?
  • Due oggetti sono simili se la loro distanza è molto bassa

Quindi i gruppo dovranno essere compatti e separati ciascuno dagli altri.

K-means

come misura di somiglianza viene utilizzata la distanza euclidea

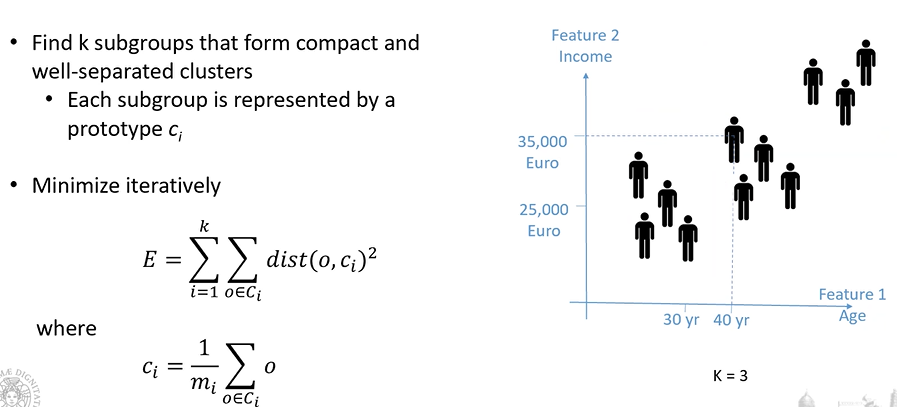
L’algoritmo minimizza la funzione di costo E definita come la sommatoria di distanza tra gli oggetti che appartengono al cluster e quello che rappresenta il cluster:

• K: numero di cluster che vogliamo determinare
• dist: distanza euclidea
• o: oggetti che appartengono alla classe C
• C_i: centroide

  • La media di tutti gli oggetti che appartengono al cluster, ovvero l’oggetto che in qualche modo è rappresentativo del nostro cluster:

    

Pseudo-codice

Problematiche

1. I Centroidi vengono selezioniati in maniera casuale. Questo non è banale perché potrebbero esserci dei minimi locali della funzione di costo che andrebbero a falsare la nostra minimizzazione durante l’algoritmo
   1. Per ovviare questo problema si può ripetere più volte il k-means per trovare la minimizzazione corretta
   2. Ci sono altre metodologie in letteratura ma richiedono alte computazioni
2. La presenza di un Outlier, potrebbe far spostare il centroide del cluster in quanto viene “attratto” da esso.
   1. Per ovviare questo problema, si può prendere l’oggetto più centrale del nostro cluster, denominato Medoide, riducendo l’effetto dell’outlier.
3. Tutti i cluster individuati tramite algoritmo di K-means creano cluster di forma sferica, a causa dell’utilizzo della distanza euclidea.
4. Bisogna capire come inizializzare K, ovvero il numero di cluster che ci aspettiamo

Elbow method

Eseguiamo il k-means con un numero piccolo per poi incrementarlo iterativamente e ricalcolare il k-means, memorizzando ad ogni iterazione il valore della funzione di costo E ottenuta.

Alla fine dell’algoritmo prenderemo il valore “di gomito” individuato nel grafico rappresentato dai valori assunti dalla funzione di costo.

Nel caso in cui non esistono Cluster naturali all’interno dei nostri dati, non riuscirò a trovare un valore “di gomito”, riuscirà comunque a trovare dei cluster “artificiali” ma che non hanno un grande significato nel trend individuato.

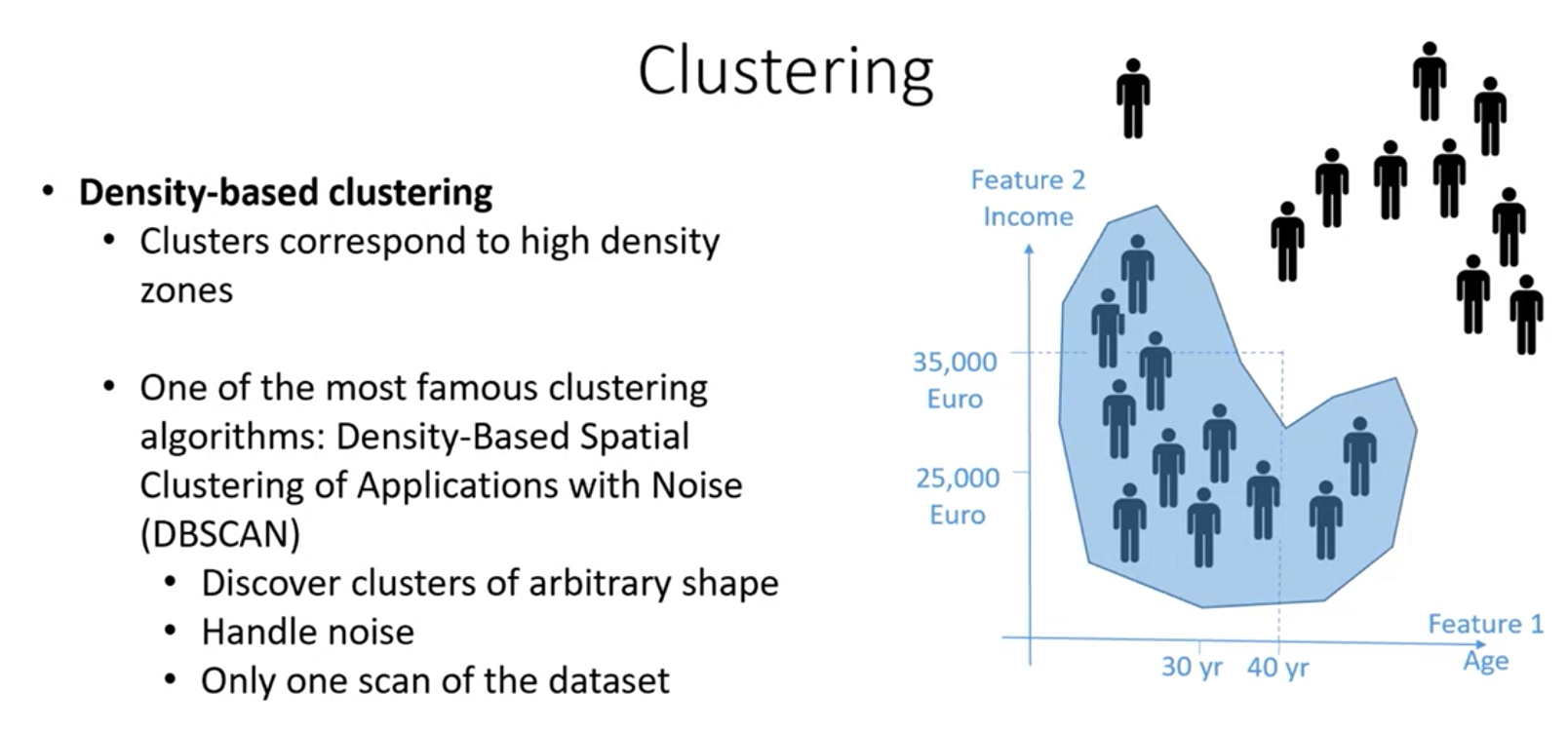
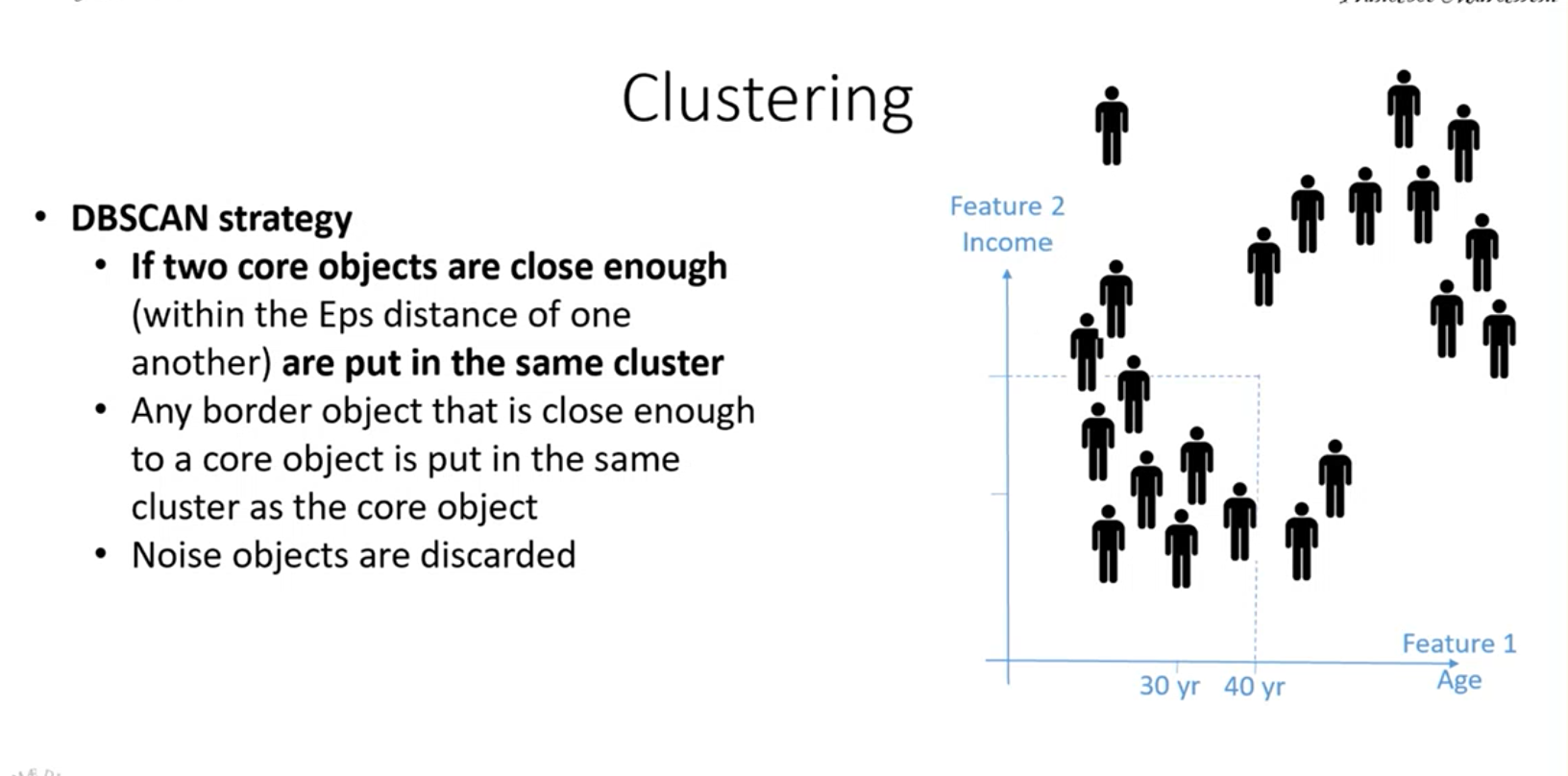
Density-based clustering (DBScan)

Vogliamo individuare cluster andando a individuare le zone dense del nostro insieme di dati, fintanto che non troviamo zone dove non abbiamo punti o una bassa densità di punti

DBscan

• Consente di scoprire cluster di qualsiasi forma dato che insegue la densità.
• Riesce a gestire il rumore perché eventuali outliar vengono effettivamente isolati.
• L’algoritmo non è iterativo, ma basta fare una scansione del dataset per avere le informazioni per costruire i cluster

Per farlo funzionare dobbiamo fissarse dei parametri, facendo ciò è come se stessimo trasmettendo la nostra idea di densità attraverso i parametri.

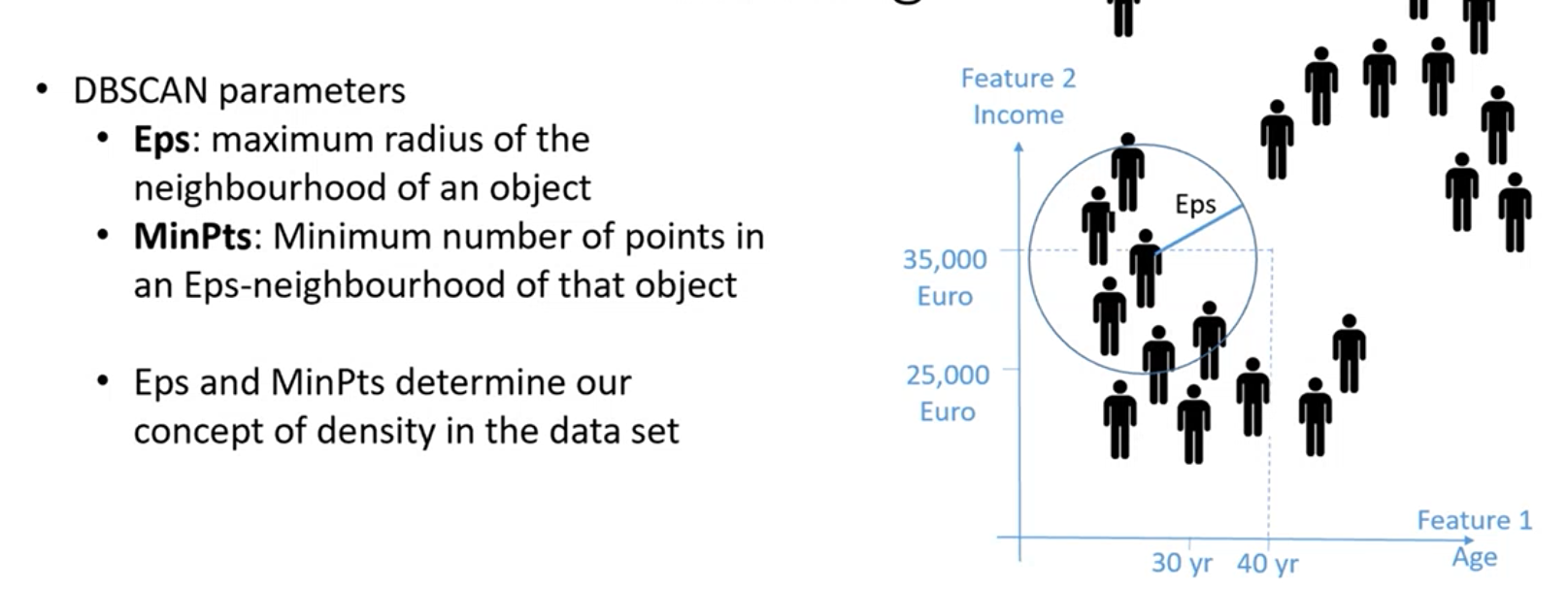
I parametri sono:

• Eps (epsilon): raggio massimo per definire il vicinato di un oggetto, quindi individuando un oggetto io fisso eps per definire qual è il vicinato, la distanza massima per cui considerare gli altri oggetti rientranti come vicinato
• MinPts: minimo numero di punti nel vicinato dell’oggetto, fisso il numero di oggetti minimo che mi aspetto all’interno del vicinato, se il numero minimo non è rispettato non è considerata una zona densa e quindi non è un cluster.

Vediamo in particolare cosa individuano questi parametri:

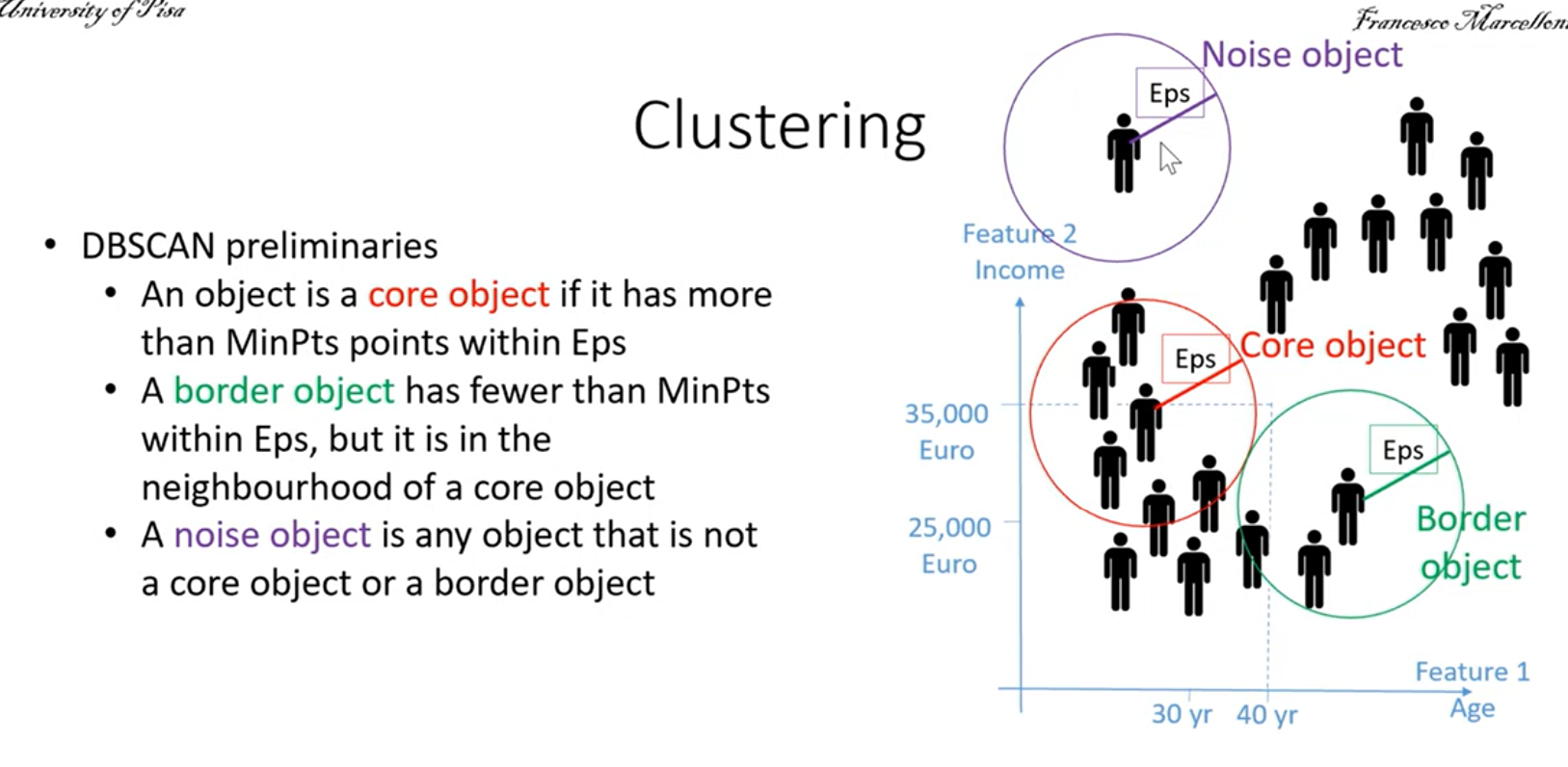
Core object: Oggetto che ha nel suo vicinato fissato da eps, un numero di punti fissato maggiore di MinPts. Ovvero si trova in una zona densa.

Boarder object: Oggetto che nel suo vicinato, non ha un numero di punti maggiore di MinPts, ma in ogni caso è nel vicinato di un oggetto core.

Noise object: Oggetto che non è core o boarder, è un oggetto isolato un out-lier.

Algoritmo DBSCAN

L’algoritmo parte individuando a caso un oggetto, se questo oggetto è un oggetto core, vede il suo vicinato, se il vicinato ha oggetti core, questi oggetti vengono inclusi, compresi i vicinanti di tali oggetti, finchè non si arriva a determinare degli oggetti boarder che conludono il cluster.

DBSCAN vs K-Means

Nel caso di DBSCAN dobbiamo però scegliere accuratamente i parametri:

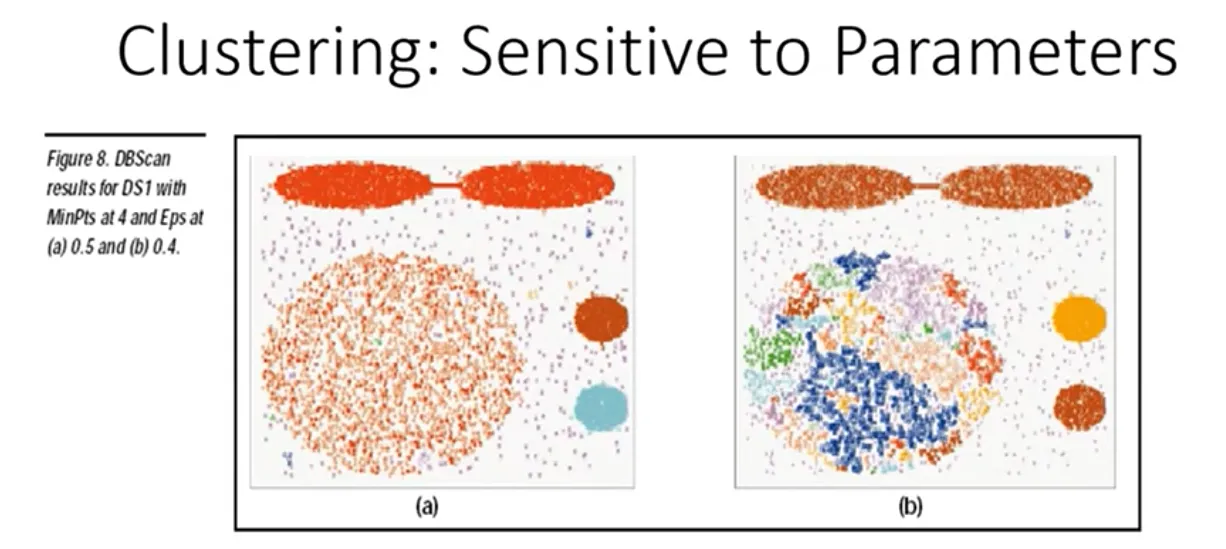
Problematiche DBSCAN

• E’ molto sensibile alla scelta dei parametri iniziali
• Se ho per tutto il DATASET la stessa densità, risco a trovare una combinazione dei parametri che va bene, ma se nello spazio ho classi con densità diversa, non è possibile trovare valire per i parametri eps e minpts che vada bene nell’intero spazio
• Quindi funziona bene quando ho cluster naturali con densità simili all’interno dello spazio

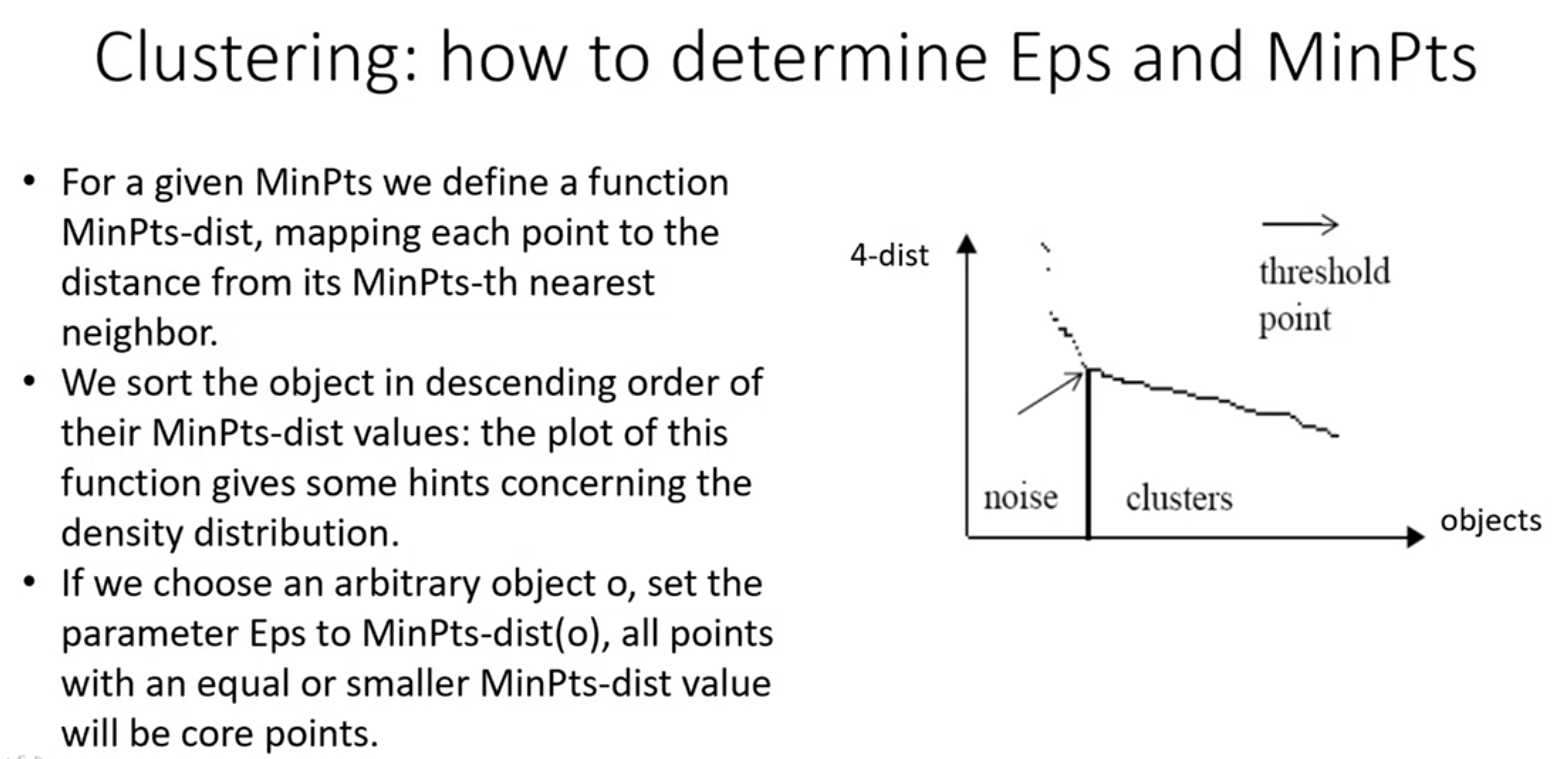
Come determino EPS e MinPts

1. Uno dei modi è quello di fissare un valore per MinPts, ci poniamo il problema di trovare EPS per quel determinato MinPts.
2. Determiniamo la distanza di ogni punto dal suo MinPts-esimo vicino, se considoer MinPts = 4, prendo il 4 ultimo vicino, e calcolo la distanza del punto che sto considerando con questo 4 punto vicino.
3. Lo faccio per tutti i punti dell’insieme di dati, e successivamente vado a Plottare queste distanze in un grafico, ordinando gli oggetti per ordine discendente dei loro valori di questa distanza.
4. Mi aspetto di ottenere un plot simile a quello nella figura sopra, se fissassi EPS in corrsipondenza della freccia, io sono sicuro che tutti gli oggetti alla destra, sono oggetti core, in quanto avranno almeno 4 punti all’interno della sfera prefissata. I punti a sinistra, non è detto che siano outlier, potrebbero essere anche dei punti boarder.
5. Cerco quindi di trovare un EPS, per cui i punti boarder ed outlier siano solo una minima parte dell’insieme di dati

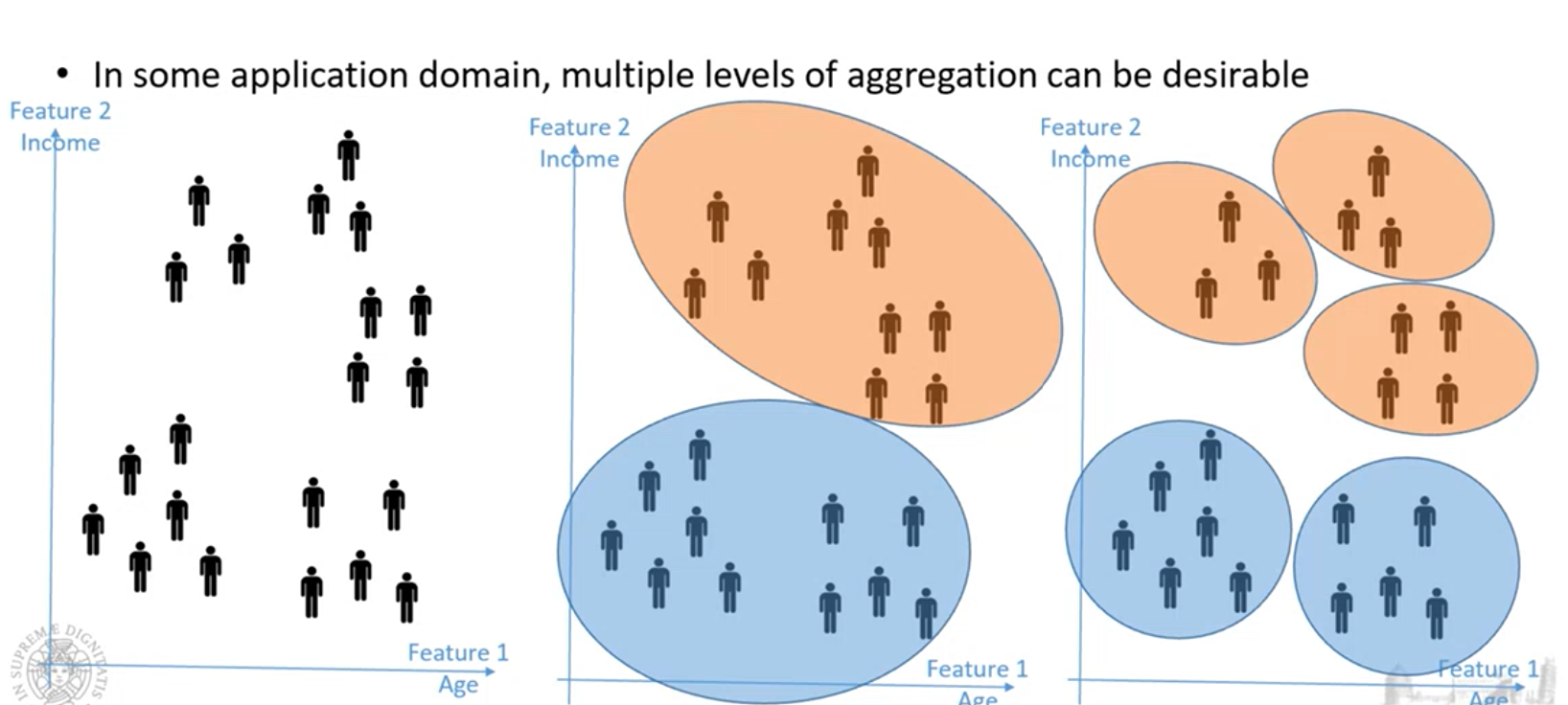
Hierarchial Clustering

Algoritmi gerarchici, creano una gerarchia di Cluster.

L’idea è partire da un insieme di dati e creare partizioni che sono sempre di più definite.

Questo consente di creare una gerarchia di cluster, in quanto parte da un cluster molto grande e poi lo divido in cluster più definiti.

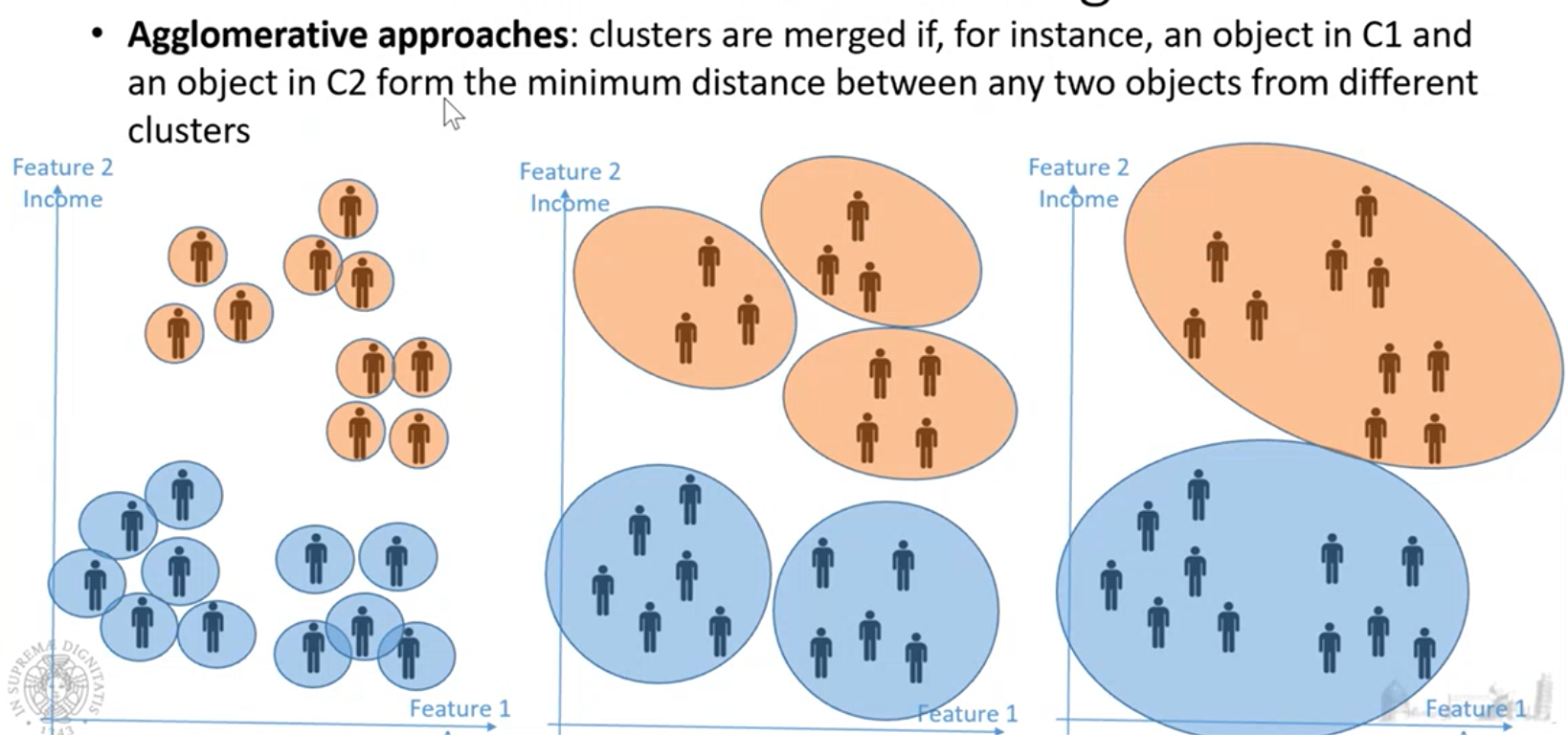
Approccio agglomerativo

parto considerando di avere un cluster per ogni punto, e poi a step successivi cerco di aggregare i cluster. Questo processo è guidado andando ad aggregare cluster che sono cluster più vicini, introducendo una distanza che è la distanza fra cluster.

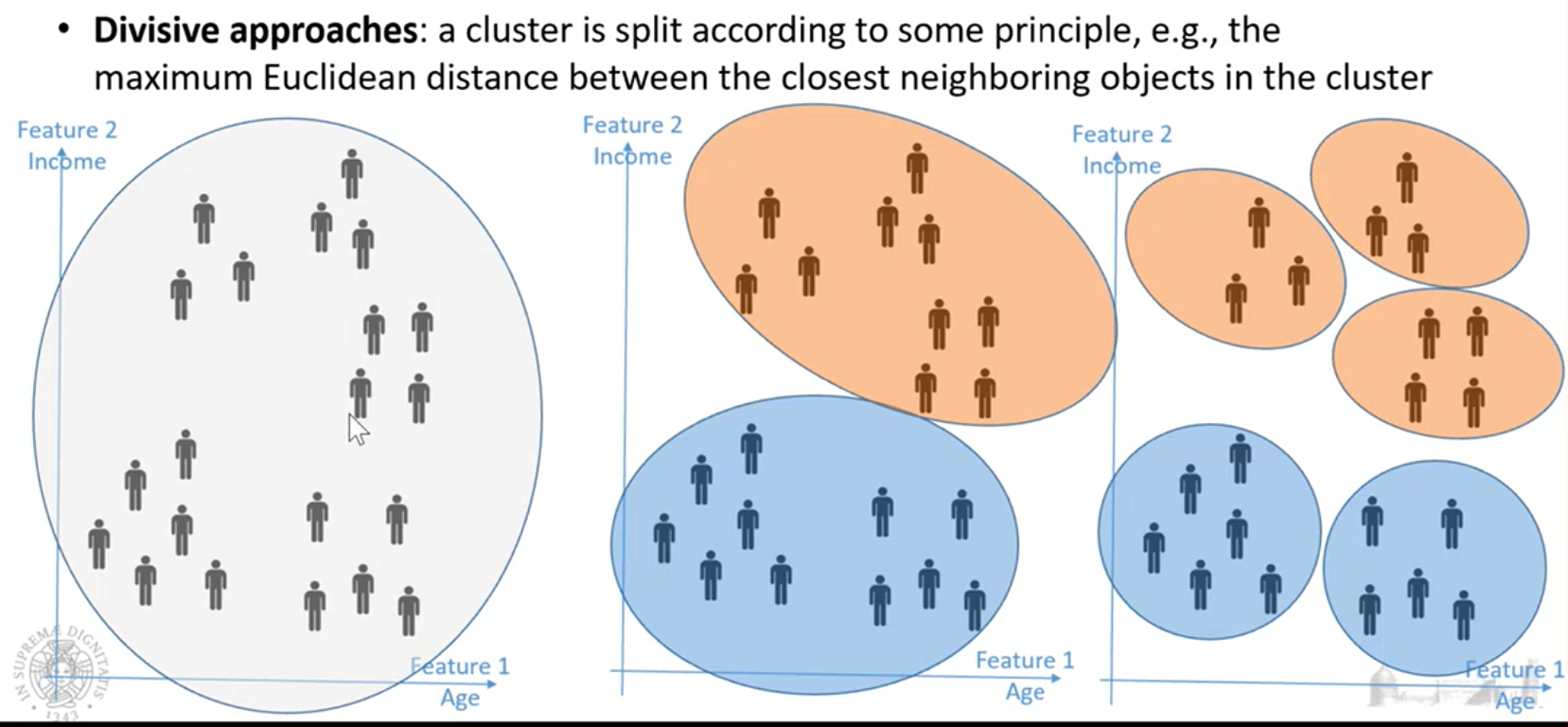
Approccio divisivo

Parto dall’avere tutto l’insieme di dati in un cluster, poi divido questo cluster in sottocluster sempre più piccoli.

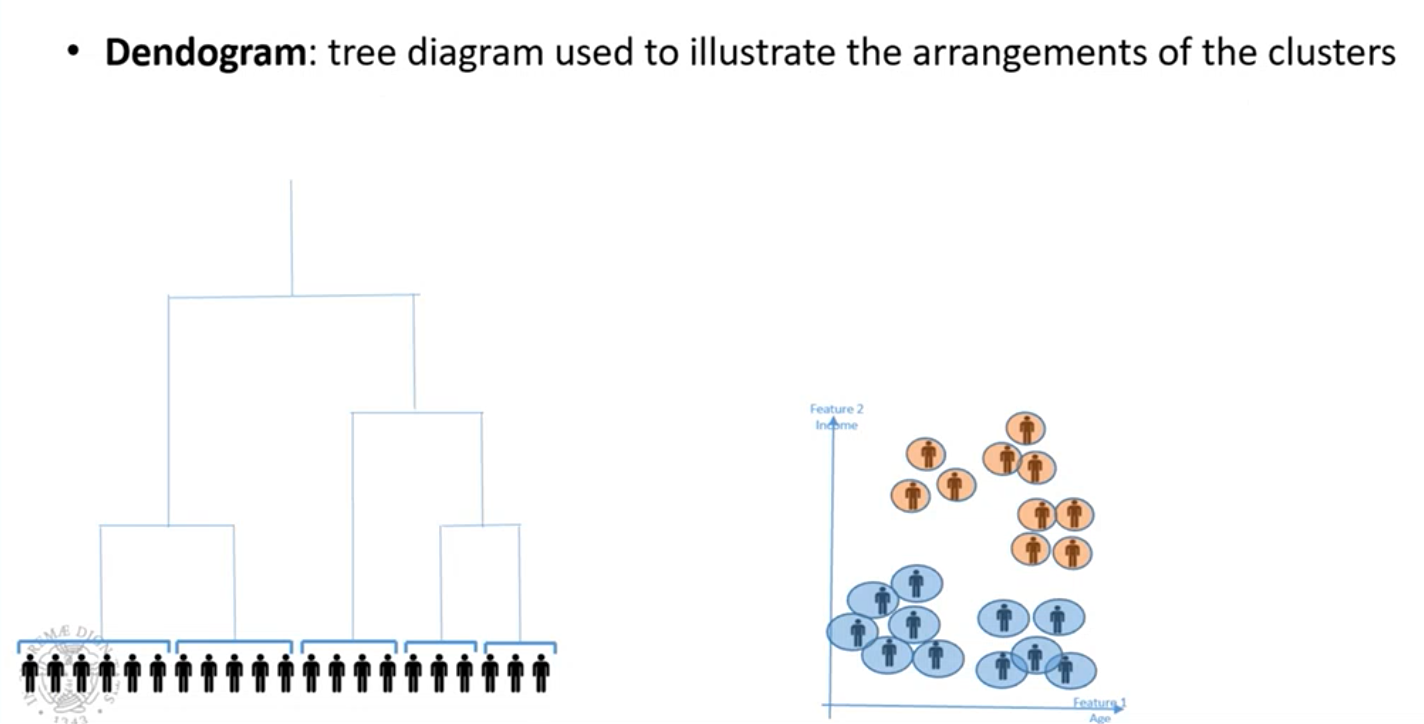
Dendogramma

Albero che descrive come i cluster sono organizzati gerarchicamente

Metriche di Clustering

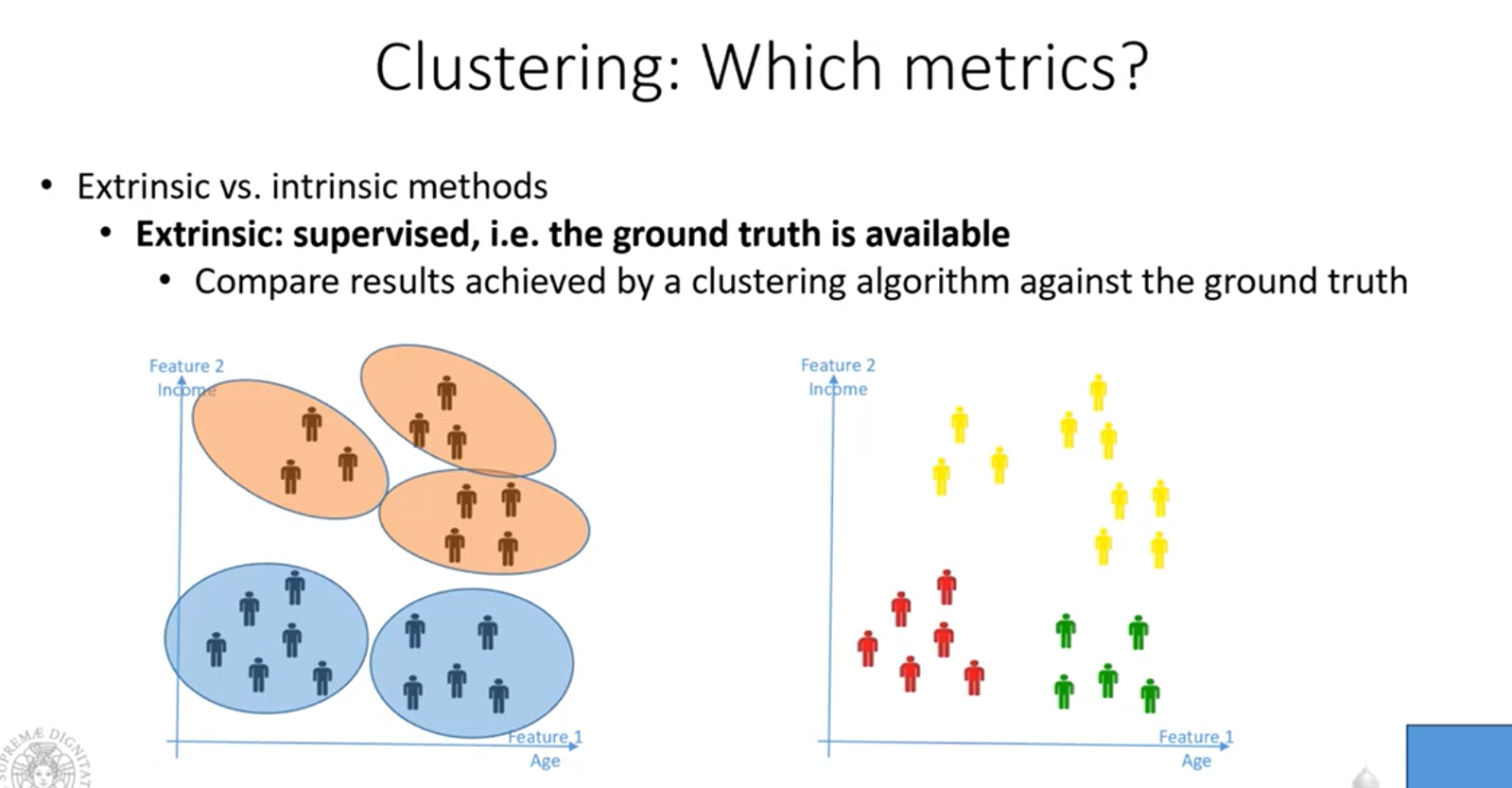
C’è un modo per capire qual è l’agoritmo di clustering che sta funzionando meglio?

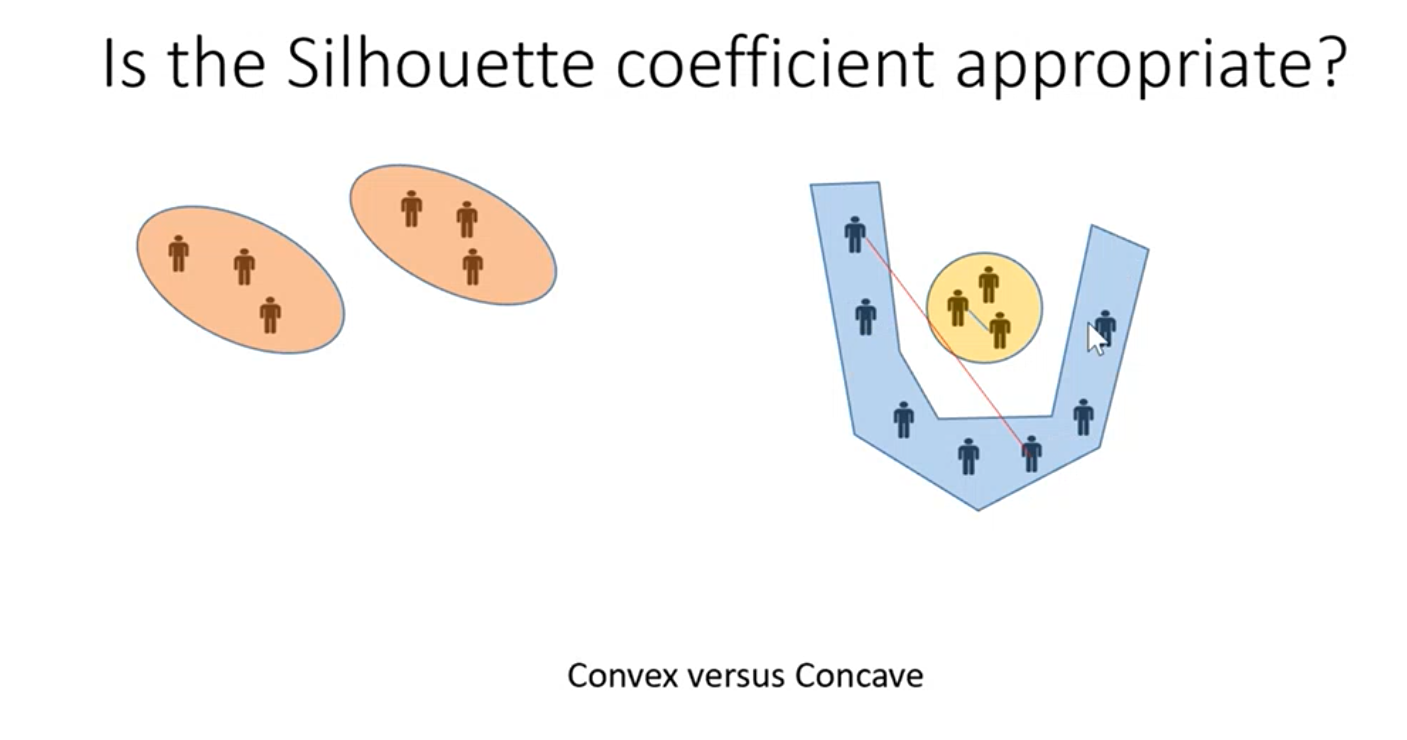
il coefficiente silhouette funziona bene solo se possiamo assumere che i cluster sono tutti convessi. Se ci sono cluster concavi il coefficiente non funziona più bene.

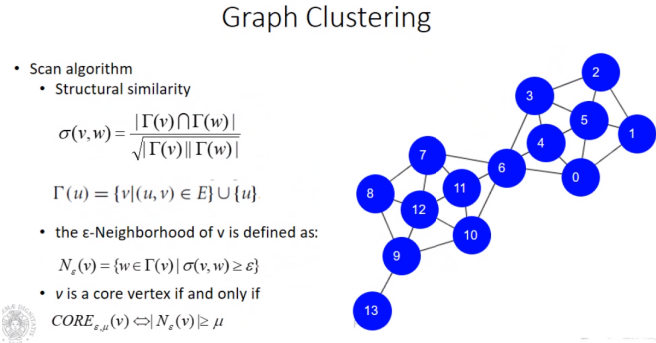
Graph Clustering

L’analisi dei grafi permette di rappresentare le relazioni che esistono nelle reti sociali, rappresentando attraverso grafi, potremmo rappresentare le persone come nodi e le loro relazioni sociali con degli archi trovando se esistono dei gruppi di nodi che sono fortemente connessi.

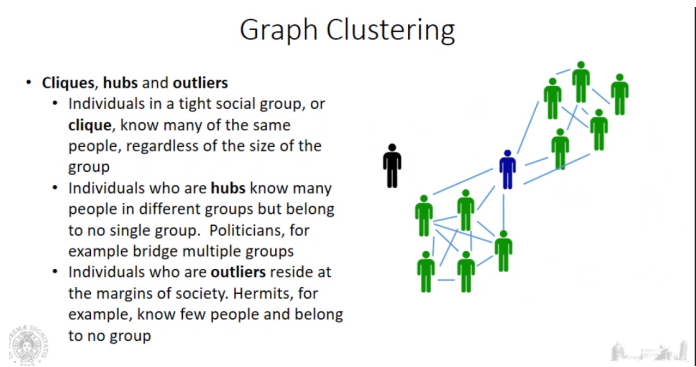
Esistono tipicamente 3 tipologie di nodi: clique: nodi effettivamente all’interno di cluster hub: oppure nodi che appartengono a tanti gruppi ma che non appartengono a nessuno, indicati in blu in figura outlier: nodi che risiedono ai margini delle relazioni

Per determinare clique, hub e outlier esistono 2 tipi di algoritmi:

• quelli che si basano sulla seguente considerazione: si introduce una funzione di somiglianza tra nodi applicando poi algoritmi di clustering tradizionali.
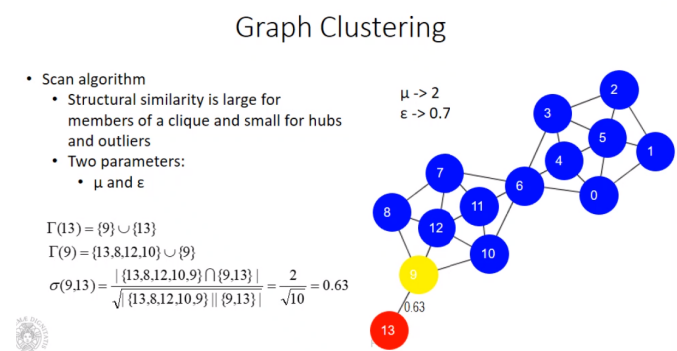
• definiscono un algoritmo basandosi direttamente sul grafo come ad esempio lo Scan algorithm. Questo algoritmo è simile al DBSCAN ma ovviamente la densità non si misura con eps e minpts ma fissando quanto un nodo sia collegato con altri nodi.

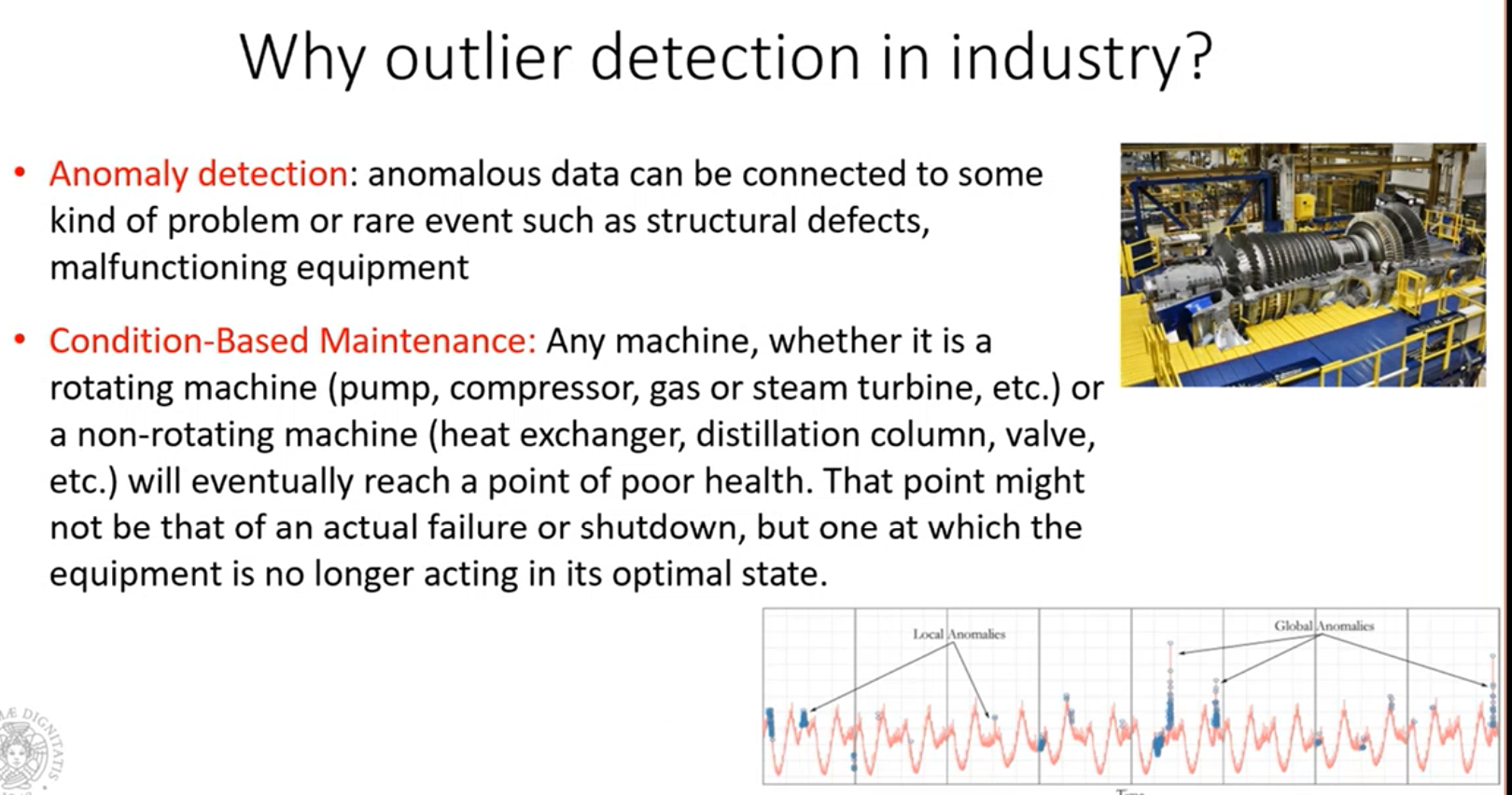
Outliers

un outlier è un oggetto devia significatamente dalla maggior parte degli oggetti nel nostro insieme di dati.

Dobbiamo stare attenti a non confondere un outlier da una novelty, una nuova feature.

Nel caso della novelty, inizialmente è un outlier, ma poi iniziano ad esserci oggetti che via via si avvicinano alla novelty.

Tipi di outlier

Determinare gli outlier

Cerchiamo di modellare come sono gli oggetti normali e poi andiamo a vedere quanto ogni oggetto devia dal comportamento normale. Nella slide abbiamo un certo numero di oggetti i quali possono essere modellati attraverso un approssimazione lineare ai minimi quadrati. Questa linea è il modello che ci rappresenta gli oggetti normali. Se calcolando la distanza di tutti gli oggetti rispetto a questa linea vediamo che esistono oggetti molto distanti da questa linea, allora questi saranno degli outlier. Questi sono gli approcci che vengono normalmente usati, qui vengono usati delle linee come approssimanti.

Se siamo interessati a un outlier detection, applicare un filtro di smoothing può impattare quello che abbiamo all’interno del segnale stesso. Applicare dei filtri di smoothing dunque potrebbe non farci individuare correttamente degli outlier.

Come individuare gli outliers

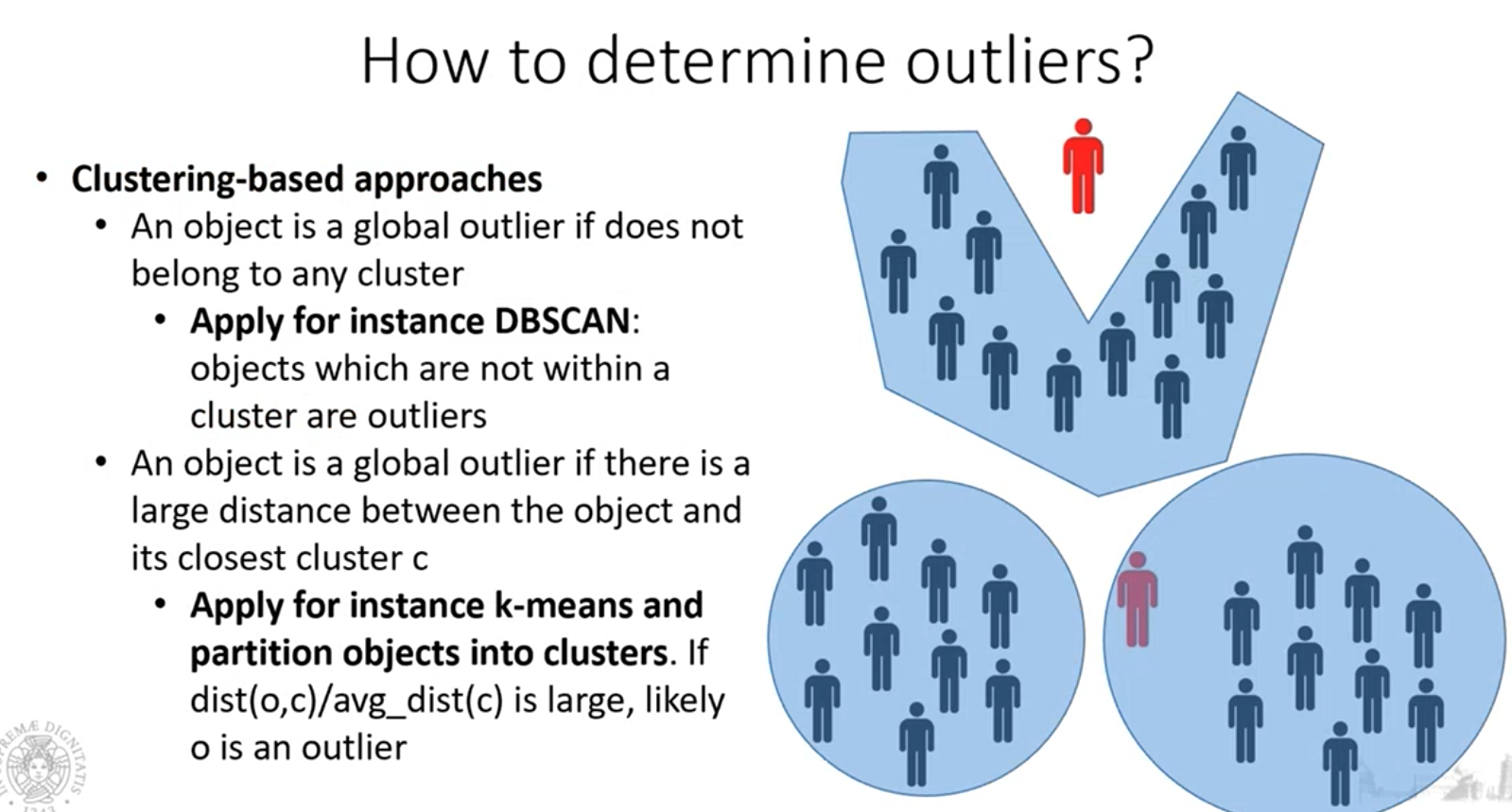
• Il DBSCAN riesce a determinare anche se ci sono degli outliers, ma non è stato pensato per individuare gli outliers ma i cluster, individuare gli outlier è un effetto “collaterale”.
• Anche il K-Means può essere applicato per determinare l’outliers, applichiamo k-means con un valore di K, valutiamo per ogni punto in un cluster, qual è la distanza tra il punto ed il centroide e la distanza media fra il centroide e tutti gli altri punti. Se il loro rapporto delle distanze calcolate (distanza punto analizzato su distanza tutti gli altri punti) è grande, allora quel punto si differenzia molto e quindi è un outlier.

Questi due approcci richiedono di fissare dei parametri. per DBSCAN parliamo di MinPts e EPS, nel caso del K-Means però, dobbiamo definire anche una soglia per cui il rapprto fra le distanze calcolate sia considerato grande, e quindi per individuare gli outliers.

Approccio density-based

Perché parliamo di individuare gli outlier?

Frequent Pattaern Analysis